Question Number 6045 by sanusihammed last updated on 10/Jun/16

$$\mathrm{4}^{{x}} \:=\:\mathrm{2}{x} \\ $$$$ \\ $$$${find}\:{x} \\ $$
Commented by Yozzii last updated on 10/Jun/16
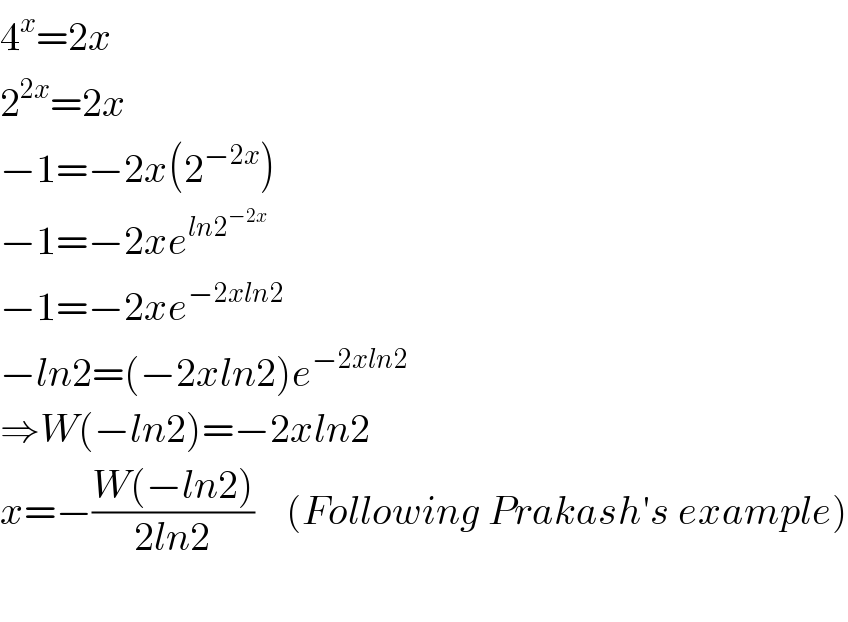
$$\mathrm{4}^{{x}} =\mathrm{2}{x} \\ $$$$\mathrm{2}^{\mathrm{2}{x}} =\mathrm{2}{x} \\ $$$$−\mathrm{1}=−\mathrm{2}{x}\left(\mathrm{2}^{−\mathrm{2}{x}} \right) \\ $$$$−\mathrm{1}=−\mathrm{2}{xe}^{{ln}\mathrm{2}^{−\mathrm{2}{x}} } \\ $$$$−\mathrm{1}=−\mathrm{2}{xe}^{−\mathrm{2}{xln}\mathrm{2}} \\ $$$$−{ln}\mathrm{2}=\left(−\mathrm{2}{xln}\mathrm{2}\right){e}^{−\mathrm{2}{xln}\mathrm{2}} \\ $$$$\Rightarrow{W}\left(−{ln}\mathrm{2}\right)=−\mathrm{2}{xln}\mathrm{2} \\ $$$${x}=−\frac{{W}\left(−{ln}\mathrm{2}\right)}{\mathrm{2}{ln}\mathrm{2}}\:\:\:\:\left({Following}\:{Prakash}'{s}\:{example}\right) \\ $$$$ \\ $$
Answered by Yozzii last updated on 11/Jun/16

$${x}=−\frac{{W}\left(−{ln}\mathrm{2}\right)}{\mathrm{2}{ln}\mathrm{2}} \\ $$
