Question Number 137139 by peter frank last updated on 30/Mar/21

Answered by Dwaipayan Shikari last updated on 30/Mar/21
![∫_1 ^e (1/((1+log(x))))−(1/((1+log(x))^2 ))dx log(x)=t =∫_0 ^1 (e^t /((1+t)))−(e^t /((1+t)^2 ))dt =[(e^t /((1+t)))]_0 ^1 =(e/2)−1 Generally ∫e^t (f(t)+f′(t))dt=e^t f(t)+C](https://www.tinkutara.com/question/Q137140.png)
$$\int_{\mathrm{1}} ^{{e}} \frac{\mathrm{1}}{\left(\mathrm{1}+{log}\left({x}\right)\right)}−\frac{\mathrm{1}}{\left(\mathrm{1}+{log}\left({x}\right)\right)^{\mathrm{2}} }{dx}\:\:\:\:\:{log}\left({x}\right)={t} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{{t}} }{\left(\mathrm{1}+{t}\right)}−\frac{{e}^{{t}} }{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt} \\ $$$$=\left[\frac{{e}^{{t}} }{\left(\mathrm{1}+{t}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{{e}}{\mathrm{2}}−\mathrm{1} \\ $$$$\boldsymbol{{Generally}}\:\int\boldsymbol{{e}}^{\boldsymbol{{t}}} \left(\boldsymbol{{f}}\left(\boldsymbol{{t}}\right)+\boldsymbol{{f}}'\left(\boldsymbol{{t}}\right)\right)\boldsymbol{{dt}}=\boldsymbol{{e}}^{\boldsymbol{{t}}} \boldsymbol{{f}}\left(\boldsymbol{{t}}\right)+{C} \\ $$
Commented by Ar Brandon last updated on 30/Mar/21
![∫e^(g(x)) [f(x)g′(x)+f ′(x)]dx=e^(g(x)) f(x)+C](https://www.tinkutara.com/question/Q137144.png)
$$\int\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{g}}\left(\boldsymbol{\mathrm{x}}\right)} \left[\boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{g}}'\left(\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathrm{f}}\:'\left(\boldsymbol{\mathrm{x}}\right)\right]\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{g}}\left(\boldsymbol{\mathrm{x}}\right)} \boldsymbol{\mathrm{f}}\left(\boldsymbol{\mathrm{x}}\right)+\boldsymbol{\mathcal{C}} \\ $$
Commented by Dwaipayan Shikari last updated on 30/Mar/21
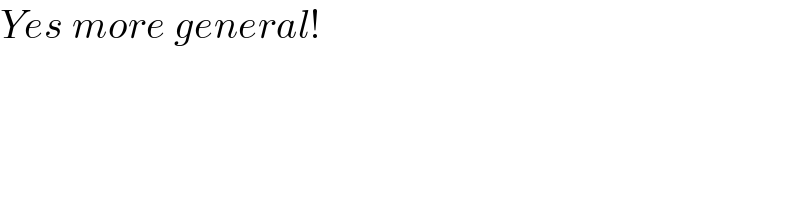
$${Yes}\:{more}\:{general}! \\ $$
