Question Number 61349 by tanmay last updated on 01/Jun/19

Commented by MJS last updated on 01/Jun/19
![...harder than I thought ∫((√(t^2 −5))/(t−a))dt= [t=((√5)/(sin u)) ⇔ u=arcsin ((√5)/t) → dt=−((t(√(t^2 −5)))/( (√5)))du] now the root is gone, but we must make another substitution, I want to make it in one step [u=2arctan v ⇔ v=tan (u/2) → du=2cos^2 (u/2)] ⇒ [t=(((v^2 +1)(√5))/(2v)) ⇔ v=((√5)/5)(t+(√(t^2 −5))) → dt=((√(5(t^2 −5)))/(t+(√(t^2 −5))))] =((√5)/2)∫(((v^2 −1)^2 )/(v^2 (v^2 −((2a)/( (√5)))v+1)))dv I_1 =∫((√(t^2 −5))/(t−3))dt=((√5)/2)∫(((v^2 −1)^2 )/(v^2 (v−(√5))(v−(1/( (√5))))))dv I_2 =∫((√(t^2 −5))/(t−1))dt=((√5)/2)∫(((v^2 −1)^2 )/(v^2 (v^2 −(2/( (√5)))v+1)))dv now decompose and solve I_1 =((√5)/2)(v−(1/v))+3ln v +2ln (v−(√5)) −2ln (5v−(√5)) I_2 =((√5)/2)(v−(1/v))+ln v +4arctan ((1−(√5)v)/2)](https://www.tinkutara.com/question/Q61367.png)
$$…\mathrm{harder}\:\mathrm{than}\:\mathrm{I}\:\mathrm{thought} \\ $$$$\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{{t}−{a}}{dt}= \\ $$$$\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{5}}}{\mathrm{sin}\:{u}}\:\Leftrightarrow\:{u}=\mathrm{arcsin}\:\frac{\sqrt{\mathrm{5}}}{{t}}\:\rightarrow\:{dt}=−\frac{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{\:\sqrt{\mathrm{5}}}{du}\right] \\ $$$$\:\:\:\:\:\mathrm{now}\:\mathrm{the}\:\mathrm{root}\:\mathrm{is}\:\mathrm{gone},\:\mathrm{but}\:\mathrm{we}\:\mathrm{must}\:\mathrm{make} \\ $$$$\:\:\:\:\:\mathrm{another}\:\mathrm{substitution},\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{make}\:\mathrm{it} \\ $$$$\:\:\:\:\:\mathrm{in}\:\mathrm{one}\:\mathrm{step} \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{2arctan}\:{v}\:\Leftrightarrow\:{v}=\mathrm{tan}\:\frac{{u}}{\mathrm{2}}\:\rightarrow\:{du}=\mathrm{2cos}^{\mathrm{2}} \:\frac{{u}}{\mathrm{2}}\right] \\ $$$$\:\:\:\:\:\Rightarrow \\ $$$$\:\:\:\:\:\left[{t}=\frac{\left({v}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{\mathrm{5}}}{\mathrm{2}{v}}\:\Leftrightarrow\:{v}=\frac{\sqrt{\mathrm{5}}}{\mathrm{5}}\left({t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}\right)\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{5}\left({t}^{\mathrm{2}} −\mathrm{5}\right)}}{{t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}\right] \\ $$$$=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\int\frac{\left({v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{v}^{\mathrm{2}} \left({v}^{\mathrm{2}} −\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{5}}}{v}+\mathrm{1}\right)}{dv} \\ $$$${I}_{\mathrm{1}} =\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{{t}−\mathrm{3}}{dt}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\int\frac{\left({v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{v}^{\mathrm{2}} \left({v}−\sqrt{\mathrm{5}}\right)\left({v}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)}{dv} \\ $$$${I}_{\mathrm{2}} =\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{{t}−\mathrm{1}}{dt}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\int\frac{\left({v}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{{v}^{\mathrm{2}} \left({v}^{\mathrm{2}} −\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}{v}+\mathrm{1}\right)}{dv} \\ $$$$\mathrm{now}\:\mathrm{decompose}\:\mathrm{and}\:\mathrm{solve} \\ $$$${I}_{\mathrm{1}} =\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left({v}−\frac{\mathrm{1}}{{v}}\right)+\mathrm{3ln}\:{v}\:+\mathrm{2ln}\:\left({v}−\sqrt{\mathrm{5}}\right)\:−\mathrm{2ln}\:\left(\mathrm{5}{v}−\sqrt{\mathrm{5}}\right) \\ $$$${I}_{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\left({v}−\frac{\mathrm{1}}{{v}}\right)+\mathrm{ln}\:{v}\:+\mathrm{4arctan}\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}{v}}{\mathrm{2}} \\ $$
Commented by tanmay last updated on 01/Jun/19

$${source}\:{goiit} \\ $$
Commented by MJS last updated on 01/Jun/19
![(1/((x^2 −x+1)+(√(x^4 −4x^3 +9x^2 −10x+5))))= =(((x^2 −x+1)−(√(x^4 −4x^3 +9x^2 −10x+5)))/(2(x−1)(x^2 −2x+2)))= =(1/(2(x−1)))+(1/(2(x^2 −2x+2)))−((√(x^4 −4x^3 +9x^2 −10x+5))/(2(x−1)(x^2 −2x+2))) ∫(dx/(x−1))=ln ∣x−1∣ ∫(dx/(x^2 −2x+2))=∫(dx/((x−1)^2 +1))=arctan (x−1) (x^2 −2x+a)^2 =x^4 −4x^3 +2(a+2)x^2 −4ax+a^2 2(a+2)=9 ⇒ a=(5/2) −4a=−10 ⇒ a=(5/2) ⇒ x^4 −4x^3 +9x^2 −10x+5=(x^2 −2x+(5/2))^2 −(5/4) ∫((√(x^4 −4x^3 +9x^2 −10x+5))/(2(x−1)(x^2 −2x+2)))dx= [t=2x^2 −4x+5 → dx=(dt/(4(x−1)))] =∫((√(t^2 −5))/(4(t−3)(t−1)))dt= =∫((√(t^2 −5))/(8(t−3)))dt−∫((√(t^2 −5))/(8(t−1)))dt this should be possible, sorry I′m running out of time](https://www.tinkutara.com/question/Q61359.png)
$$\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\sqrt{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}}}= \\ $$$$=\frac{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)−\sqrt{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}}}{\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right)}−\frac{\sqrt{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}}}{\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right)} \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}−\mathrm{1}}=\mathrm{ln}\:\mid{x}−\mathrm{1}\mid \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}}=\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}}=\mathrm{arctan}\:\left({x}−\mathrm{1}\right) \\ $$$$ \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}+{a}\right)^{\mathrm{2}} ={x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}\left({a}+\mathrm{2}\right){x}^{\mathrm{2}} −\mathrm{4}{ax}+{a}^{\mathrm{2}} \\ $$$$\mathrm{2}\left({a}+\mathrm{2}\right)=\mathrm{9}\:\Rightarrow\:{a}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$−\mathrm{4}{a}=−\mathrm{10}\:\Rightarrow\:{a}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\Rightarrow\:{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}=\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\frac{\mathrm{5}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\int\frac{\sqrt{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}}}{\mathrm{2}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}\right)}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{4}\left({x}−\mathrm{1}\right)}\right] \\ $$$$=\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{\mathrm{4}\left({t}−\mathrm{3}\right)\left({t}−\mathrm{1}\right)}{dt}= \\ $$$$=\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{\mathrm{8}\left({t}−\mathrm{3}\right)}{dt}−\int\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{5}}}{\mathrm{8}\left({t}−\mathrm{1}\right)}{dt} \\ $$$$\mathrm{this}\:\mathrm{should}\:\mathrm{be}\:\mathrm{possible},\:\mathrm{sorry}\:\mathrm{I}'\mathrm{m}\:\mathrm{running} \\ $$$$\mathrm{out}\:\mathrm{of}\:\mathrm{time} \\ $$
Commented by MJS last updated on 01/Jun/19
$$\mathrm{Sir}\:\mathrm{Tanmay},\:\mathrm{please}\:\mathrm{try}\:\mathrm{to}\:\mathrm{complete}\:\mathrm{this} \\ $$
Commented by tanmay last updated on 01/Jun/19
$${yes}\:{sir}..{i}\:{shall}\:{try}\:{sir}… \\ $$
Commented by MJS last updated on 01/Jun/19

$$…\mathrm{the}\:\mathrm{final}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{2}\:\left({B}\right) \\ $$
Commented by tanmay last updated on 01/Jun/19

$${thank}\:{you}\:{sir} \\ $$
Answered by tanmay last updated on 01/Jun/19
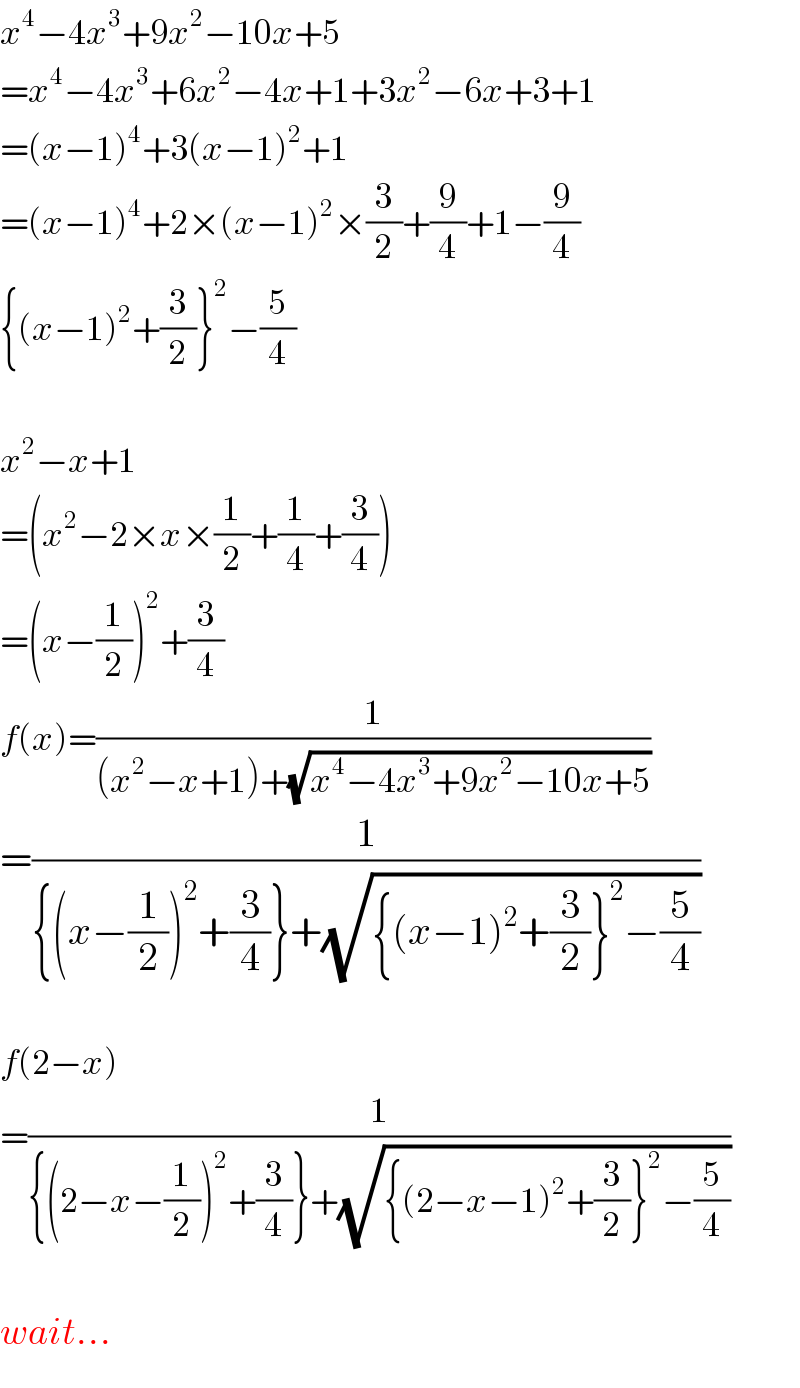
$${x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5} \\ $$$$={x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{1}+\mathrm{3}{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{3}+\mathrm{1} \\ $$$$=\left({x}−\mathrm{1}\right)^{\mathrm{4}} +\mathrm{3}\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$=\left({x}−\mathrm{1}\right)^{\mathrm{4}} +\mathrm{2}×\left({x}−\mathrm{1}\right)^{\mathrm{2}} ×\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\left\{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\right\}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$ \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1} \\ $$$$=\left({x}^{\mathrm{2}} −\mathrm{2}×{x}×\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$$$=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\sqrt{{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{3}} +\mathrm{9}{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{5}}} \\ $$$$=\frac{\mathrm{1}}{\left\{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right\}+\sqrt{\left\{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\right\}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}}} \\ $$$$ \\ $$$${f}\left(\mathrm{2}−{x}\right) \\ $$$$=\frac{\mathrm{1}}{\left\{\left(\mathrm{2}−{x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}\right\}+\sqrt{\left\{\left(\mathrm{2}−{x}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{2}}\right\}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{4}}}} \\ $$$$ \\ $$$${wait}… \\ $$
