Question Number 71611 by ajfour last updated on 17/Oct/19

Commented by ajfour last updated on 17/Oct/19

$${Find}\:{time}\:{it}\:{takes}\:{the}\:{cylinder} \\ $$$${to}\:{unwind}\:{and}\:{slide}\:{and}\:{hit}\:{the} \\ $$$${ground}. \\ $$
Commented by ajfour last updated on 18/Oct/19

Answered by Tanmay chaudhury last updated on 18/Oct/19
![mg−Tcosα=ma Tsinα=N T.r=I((a/r))→T=((Ia)/r^2 ) mg−((Iacosα)/r^2 )=ma a(((Icosα)/r^2 )+m)=mg a=((mg)/(((Icosα)/r^2 )+m))→h=(1/2)at^2 →t=(√((2h)/a)) t=(√(((2h)/(mg))×(m+((Icosα)/r^2 )) )) t=(√(((2h)/(mg))×(m+((mr^2 cosα)/(2r^2 ))))) [I=((mr^2 )/2)] t=(√(((2h)/(mg))×m(1+((r^2 cosα)/(2r^2 ))))) t=(√(((2h)/g)×(1+((cosα)/2)))) pls check is it correct...](https://www.tinkutara.com/question/Q71675.png)
$${mg}−{Tcos}\alpha={ma} \\ $$$${Tsin}\alpha={N} \\ $$$${T}.{r}={I}\left(\frac{{a}}{{r}}\right)\rightarrow{T}=\frac{{Ia}}{{r}^{\mathrm{2}} } \\ $$$${mg}−\frac{{Iacos}\alpha}{{r}^{\mathrm{2}} }={ma} \\ $$$${a}\left(\frac{{Icos}\alpha}{{r}^{\mathrm{2}} }+{m}\right)={mg} \\ $$$${a}=\frac{{mg}}{\frac{{Icos}\alpha}{{r}^{\mathrm{2}} }+{m}}\rightarrow{h}=\frac{\mathrm{1}}{\mathrm{2}}{at}^{\mathrm{2}} \rightarrow{t}=\sqrt{\frac{\mathrm{2}{h}}{{a}}} \\ $$$${t}=\sqrt{\frac{\mathrm{2}{h}}{{mg}}×\left({m}+\frac{{Icos}\alpha}{{r}^{\mathrm{2}} }\right)\:} \\ $$$${t}=\sqrt{\frac{\mathrm{2}{h}}{{mg}}×\left({m}+\frac{{mr}^{\mathrm{2}} {cos}\alpha}{\mathrm{2}{r}^{\mathrm{2}} }\right)}\:\left[{I}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}\right] \\ $$$${t}=\sqrt{\frac{\mathrm{2}{h}}{{mg}}×{m}\left(\mathrm{1}+\frac{{r}^{\mathrm{2}} {cos}\alpha}{\mathrm{2}{r}^{\mathrm{2}} }\right)}\: \\ $$$${t}=\sqrt{\frac{\mathrm{2}{h}}{{g}}×\left(\mathrm{1}+\frac{{cos}\alpha}{\mathrm{2}}\right)}\: \\ $$$$ \\ $$$$\boldsymbol{{pls}}\:{c}\boldsymbol{{heck}}\:\boldsymbol{{is}}\:\boldsymbol{{it}}\:\boldsymbol{{correct}}… \\ $$$$ \\ $$
Commented by Tanmay chaudhury last updated on 18/Oct/19
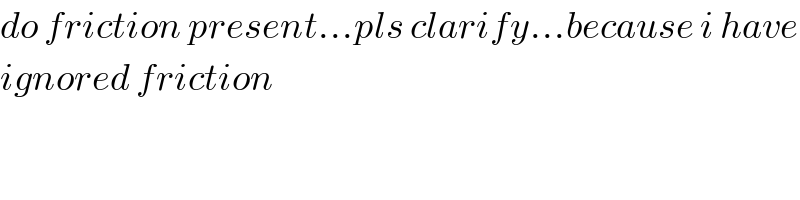
$${do}\:{friction}\:{present}…{pls}\:{clarify}…{because}\:{i}\:{have} \\ $$$${ignored}\:{friction} \\ $$
Commented by ajfour last updated on 19/Oct/19
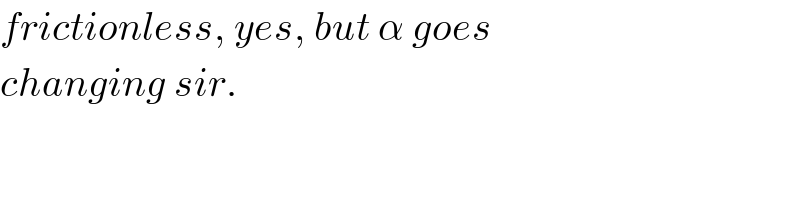
$${frictionless},\:{yes},\:{but}\:\alpha\:{goes} \\ $$$${changing}\:{sir}. \\ $$
Answered by mr W last updated on 19/Oct/19

Commented by mr W last updated on 19/Oct/19
![i use β to replace α in the question AC=h+(r/(tan (β/2)))=s+(r/(tan (θ/2)))=k tan (θ/2)=(r/(k−s)) cos θ=((1−((r/(k−s)))^2 )/(1+((r/(k−s)))^2 ))=1−((2r^2 )/((k−s)^2 +r^2 )) mg−T cos θ=ma Tr=Iα I=((mr^2 )/2) α=(a/r) Tr=((mr^2 )/2)×(a/r) T=((ma)/2) mg−((ma cos θ)/2)=ma ⇒a=((2g)/(2+cos θ))=((2g)/(3−((2r^2 )/((k−s)^2 +r^2 ))))=((2g[(k−s)^2 +r^2 ])/(3(k−s)^2 +r^2 )) ⇒−v(dv/ds)=2g×(((k−s)^2 +r^2 )/(3(k−s)^2 +r^2 )) ⇒∫_0 ^v vdv=−2g∫_h ^s (((k−s)^2 +r^2 )/(3(k−s)^2 +r^2 ))ds ⇒(v^2 /2)=2g∫_h ^s (((k−s)^2 +r^2 )/(3(k−s)^2 +r^2 ))d(k−s) ⇒(v^2 /(4g))=∫_(k−h) ^(k−s) ((u^2 +r^2 )/(3u^2 +r^2 ))du ⇒(v^2 /(4g))=(1/3)[((2r)/( (√3))) tan^(−1) (((√3)u)/r)+u]_(k−h) ^(k−s) ⇒(v^2 /(4g))=(1/3)[((2r)/( (√3)))(tan^(−1) ((√3)/(tan (θ/2)))−tan^(−1) ((√3)/(tan (β/2))))+(r/(tan (θ/2)))−(r/(tan (β/2)))] ⇒((3v^2 )/(4gr))=(2/( (√3)))(tan^(−1) ((√3)/(tan (θ/2)))−tan^(−1) ((√3)/(tan (β/2))))+(1/(tan (θ/2)))−(1/(tan (β/2))) ⇒v=((2(√(gr)))/( (√3)))(√((2/( (√3)))(tan^(−1) ((√3)/(tan (θ/2)))−tan^(−1) ((√3)/(tan (β/2))))+(1/(tan (θ/2)))−(1/(tan (β/2))))) ⇒(ds/dt)=((2(√(gr)))/( (√3)))(√((2/( (√3)))(tan^(−1) (((√3)(k−s))/r)−tan^(−1) ((√3)/(tan (β/2))))+((k−s)/r)−(1/(tan (β/2))))) ⇒((2(√(gr)))/( (√3)))∫_0 ^t dt=∫_h ^r (ds/( (√((2/( (√3)))(tan^(−1) (((√3)(k−s))/r)−tan^(−1) ((√3)/(tan (β/2))))+((k−s)/r)−(1/(tan (β/2))))))) ⇒t=((√3)/(2(√(gr))))∫_h ^r (ds/( (√((2/( (√3)))(tan^(−1) (((√3)(k−s))/r)−tan^(−1) ((√3)/(tan (β/2))))+((k−s)/r)−(1/(tan (β/2))))))) ......](https://www.tinkutara.com/question/Q71736.png)
$${i}\:{use}\:\beta\:{to}\:{replace}\:\alpha\:{in}\:{the}\:{question} \\ $$$${AC}={h}+\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}={s}+\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}={k} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{r}}{{k}−{s}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}−\left(\frac{{r}}{{k}−{s}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{r}}{{k}−{s}}\right)^{\mathrm{2}} }=\mathrm{1}−\frac{\mathrm{2}{r}^{\mathrm{2}} }{\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$${mg}−{T}\:\mathrm{cos}\:\theta={ma} \\ $$$${Tr}={I}\alpha \\ $$$${I}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\alpha=\frac{{a}}{{r}} \\ $$$${Tr}=\frac{{mr}^{\mathrm{2}} }{\mathrm{2}}×\frac{{a}}{{r}} \\ $$$${T}=\frac{{ma}}{\mathrm{2}} \\ $$$${mg}−\frac{{ma}\:\mathrm{cos}\:\theta}{\mathrm{2}}={ma} \\ $$$$\Rightarrow{a}=\frac{\mathrm{2}{g}}{\mathrm{2}+\mathrm{cos}\:\theta}=\frac{\mathrm{2}{g}}{\mathrm{3}−\frac{\mathrm{2}{r}^{\mathrm{2}} }{\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }}=\frac{\mathrm{2}{g}\left[\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \right]}{\mathrm{3}\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\Rightarrow−{v}\frac{{dv}}{{ds}}=\mathrm{2}{g}×\frac{\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{{v}} {vdv}=−\mathrm{2}{g}\int_{{h}} ^{{s}} \frac{\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }{ds} \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2}{g}\int_{{h}} ^{{s}} \frac{\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}\left({k}−{s}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} }{d}\left({k}−{s}\right) \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{\mathrm{4}{g}}=\int_{{k}−{h}} ^{{k}−{s}} \frac{{u}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}{u}^{\mathrm{2}} +{r}^{\mathrm{2}} }{du} \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{\mathrm{4}{g}}=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{3}}}\:\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}{u}}{{r}}+{u}\right]_{{k}−{h}} ^{{k}−{s}} \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{\mathrm{4}{g}}=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{2}{r}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right)+\frac{{r}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right] \\ $$$$\Rightarrow\frac{\mathrm{3}{v}^{\mathrm{2}} }{\mathrm{4}{gr}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}} \\ $$$$\Rightarrow{v}=\frac{\mathrm{2}\sqrt{{gr}}}{\:\sqrt{\mathrm{3}}}\sqrt{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}} \\ $$$$\Rightarrow\frac{{ds}}{{dt}}=\frac{\mathrm{2}\sqrt{{gr}}}{\:\sqrt{\mathrm{3}}}\sqrt{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}\left({k}−{s}\right)}{{r}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right)+\frac{{k}−{s}}{{r}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}} \\ $$$$\Rightarrow\frac{\mathrm{2}\sqrt{{gr}}}{\:\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{{t}} {dt}=\int_{{h}} ^{{r}} \frac{{ds}}{\:\sqrt{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}\left({k}−{s}\right)}{{r}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right)+\frac{{k}−{s}}{{r}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}}} \\ $$$$\Rightarrow{t}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\sqrt{{gr}}}\int_{{h}} ^{{r}} \frac{{ds}}{\:\sqrt{\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}\left({k}−{s}\right)}{{r}}−\mathrm{tan}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}\right)+\frac{{k}−{s}}{{r}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}}} \\ $$$$…… \\ $$
Commented by ajfour last updated on 19/Oct/19

Commented by ajfour last updated on 19/Oct/19
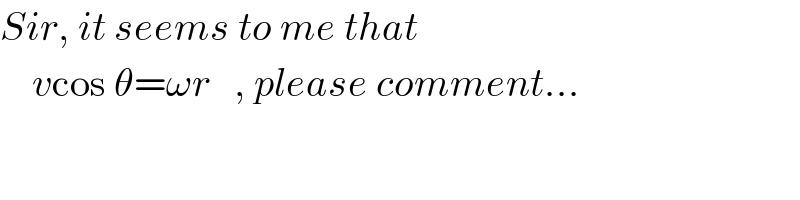
$${Sir},\:{it}\:{seems}\:{to}\:{me}\:{that} \\ $$$$\:\:\:\:{v}\mathrm{cos}\:\theta=\omega{r}\:\:\:,\:{please}\:{comment}… \\ $$
Commented by mr W last updated on 19/Oct/19

$${i}\:{thought}\:{exactly}\:{so}\:{at}\:{the}\:{begining}, \\ $$$${then}\:{i}\:{changed}\:{my}\:{mind}.\:{let}'{s}\:{say} \\ $$$${the}\:{length}\:{of}\:{wire}\:{is}\:{AD}={l}, \\ $$$${l}+{s}={k}={constant} \\ $$$${the}\:{speed}\:{of}\:{unwinding}\:\omega{r}=\frac{{dl}}{{dt}}=−\frac{{ds}}{{dt}}={v}. \\ $$$${actually}\:{i}\:{am}\:{still}\:{confused}\:{what}\:{is} \\ $$$${really}\:{true}. \\ $$
Commented by ajfour last updated on 19/Oct/19
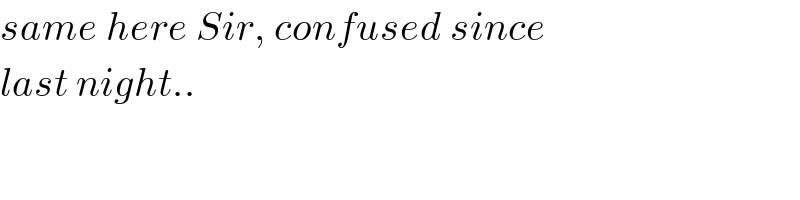
$${same}\:{here}\:{Sir},\:{confused}\:{since} \\ $$$${last}\:{night}.. \\ $$
Commented by mr W last updated on 20/Oct/19

Commented by mr W last updated on 20/Oct/19

$${i}\:{have}\:{clarified}: \\ $$$${let}\:{AB}={s} \\ $$$${v}=\frac{{ds}}{{dt}} \\ $$$${rotation}\:{of}\:{cylinder}\:{d}\varphi=\left(\theta+{d}\theta\right)+\phi−\theta=\frac{{ds}}{{r}}+{d}\theta \\ $$$${with}\:\phi=\frac{{ds}}{{r}}={rotation}\:{due}\:{to}\:{unwinding} \\ $$$$\omega=\frac{{d}\varphi}{{dt}}=\frac{{v}}{{r}}+\frac{{d}\theta}{{dt}}=\frac{{v}}{{r}}+{v}\frac{{d}\theta}{{ds}} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{r}}{{s}} \\ $$$$\frac{{d}\theta}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}=−\frac{{rds}}{{s}^{\mathrm{2}} }=−\mathrm{tan}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\frac{{ds}}{{r}} \\ $$$$\Rightarrow\frac{{d}\theta}{{ds}}=−\frac{\mathrm{1}}{{r}}\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow\omega=\frac{{v}}{{r}}+{v}\frac{{d}\theta}{{ds}}=\frac{{v}}{{r}}\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}\right)=\frac{{v}\:\mathrm{cos}\:\theta}{{r}} \\ $$$$\Rightarrow{r}\omega={v}\:\mathrm{cos}\:\theta \\ $$
Commented by mr W last updated on 20/Oct/19
![new attempt: s_0 =(r/(tan (β/2))) s_1 =(r/(tan (β/2)))+h−r mg(s−s_0 )=(1/2)mv^2 +(1/2)Iω^2 g(s−s_0 )=(1/2)v^2 +(r^2 /4)ω^2 g(s−s_0 )=(1/4)v^2 (2+cos^2 θ) tan (θ/2)=(r/s) cos θ=((1−((r/s))^2 )/(1+((r/s))^2 ))=((s^2 −r^2 )/(s^2 +r^2 )) g(s−s_0 )=(1/4)v^2 [2+(((s^2 −r^2 )/(s^2 +r^2 )))^2 ] ⇒v=2(√((g(s−s_0 ))/(2+(((s^2 −r^2 )/(s^2 +r^2 )))^2 ))) ⇒(ds/dt)=2(√g)(√((s−s_0 )/(2+(((s^2 −r^2 )/(s^2 +r^2 )))^2 ))) ⇒t=(1/(2(√g)))∫_s_0 ^s_1 (√((2+(((s^2 −r^2 )/(s^2 +r^2 )))^2 )/(s−s_0 )))ds](https://www.tinkutara.com/question/Q71797.png)
$${new}\:{attempt}: \\ $$$${s}_{\mathrm{0}} =\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}} \\ $$$${s}_{\mathrm{1}} =\frac{{r}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}+{h}−{r} \\ $$$${mg}\left({s}−{s}_{\mathrm{0}} \right)=\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{I}\omega^{\mathrm{2}} \\ $$$${g}\left({s}−{s}_{\mathrm{0}} \right)=\frac{\mathrm{1}}{\mathrm{2}}{v}^{\mathrm{2}} +\frac{{r}^{\mathrm{2}} }{\mathrm{4}}\omega^{\mathrm{2}} \\ $$$${g}\left({s}−{s}_{\mathrm{0}} \right)=\frac{\mathrm{1}}{\mathrm{4}}{v}^{\mathrm{2}} \left(\mathrm{2}+\mathrm{cos}^{\mathrm{2}} \:\theta\right) \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{{r}}{{s}} \\ $$$$\mathrm{cos}\:\theta=\frac{\mathrm{1}−\left(\frac{{r}}{{s}}\right)^{\mathrm{2}} }{\mathrm{1}+\left(\frac{{r}}{{s}}\right)^{\mathrm{2}} }=\frac{{s}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{s}^{\mathrm{2}} +{r}^{\mathrm{2}} } \\ $$$${g}\left({s}−{s}_{\mathrm{0}} \right)=\frac{\mathrm{1}}{\mathrm{4}}{v}^{\mathrm{2}} \left[\mathrm{2}+\left(\frac{{s}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{s}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\mathrm{2}} \right] \\ $$$$\Rightarrow{v}=\mathrm{2}\sqrt{\frac{{g}\left({s}−{s}_{\mathrm{0}} \right)}{\mathrm{2}+\left(\frac{{s}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{s}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow\frac{{ds}}{{dt}}=\mathrm{2}\sqrt{{g}}\sqrt{\frac{{s}−{s}_{\mathrm{0}} }{\mathrm{2}+\left(\frac{{s}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{s}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\mathrm{2}} }} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{g}}}\int_{{s}_{\mathrm{0}} } ^{{s}_{\mathrm{1}} } \sqrt{\frac{\mathrm{2}+\left(\frac{{s}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{s}^{\mathrm{2}} +{r}^{\mathrm{2}} }\right)^{\mathrm{2}} }{{s}−{s}_{\mathrm{0}} }}{ds} \\ $$
Commented by ajfour last updated on 21/Oct/19

$${Thanks}\:{sir},\:{i}\:{cant}\:{find}\:{much} \\ $$$${time}\:{to}\:{attempt}\:{myself}\:{sir},\:{i} \\ $$$${shall}\:{however}\:{try}\:{it}\:{today}.. \\ $$
