Question Number 192689 by sciencestudentW last updated on 24/May/23
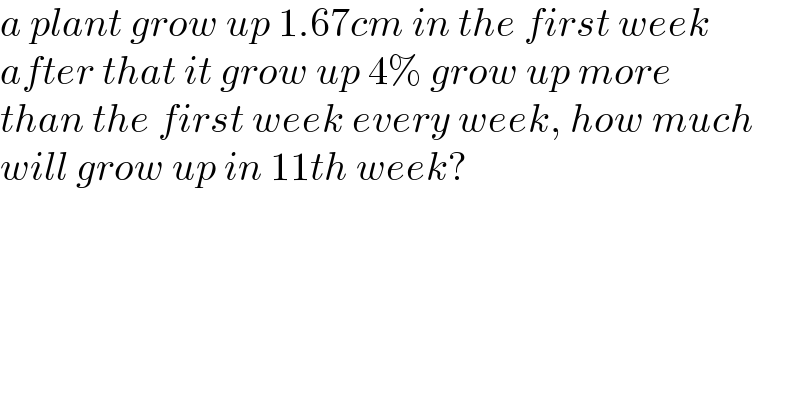
$${a}\:{plant}\:{grow}\:{up}\:\mathrm{1}.\mathrm{67}{cm}\:{in}\:{the}\:{first}\:{week} \\ $$$${after}\:{that}\:{it}\:{grow}\:{up}\:\mathrm{4\%}\:{grow}\:{up}\:{more} \\ $$$${than}\:{the}\:{first}\:{week}\:{every}\:{week},\:{how}\:{much} \\ $$$${will}\:{grow}\:{up}\:{in}\:\mathrm{11}{th}\:{week}? \\ $$
Commented by sciencestudentW last updated on 24/May/23

$$? \\ $$
Answered by Skabetix last updated on 24/May/23
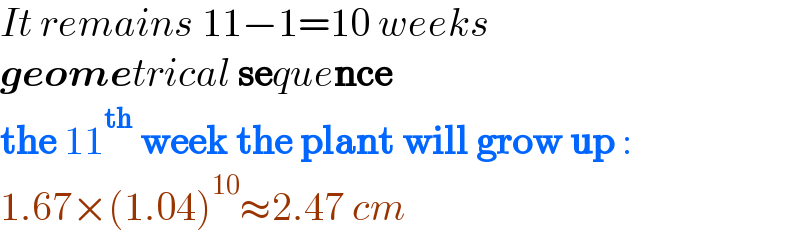
$${It}\:{remains}\:\mathrm{11}−\mathrm{1}=\mathrm{10}\:{weeks} \\ $$$$\boldsymbol{{geome}}{trical}\:\boldsymbol{\mathrm{se}}{que}\boldsymbol{\mathrm{nce}} \\ $$$$\boldsymbol{\mathrm{the}}\:\mathrm{11}^{\boldsymbol{\mathrm{th}}} \:\boldsymbol{\mathrm{week}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{plant}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{grow}}\:\boldsymbol{\mathrm{up}}\:: \\ $$$$\mathrm{1}.\mathrm{67}×\left(\mathrm{1}.\mathrm{04}\right)^{\mathrm{10}} \approx\mathrm{2}.\mathrm{47}\:{cm} \\ $$
Commented by sciencestudentW last updated on 25/May/23
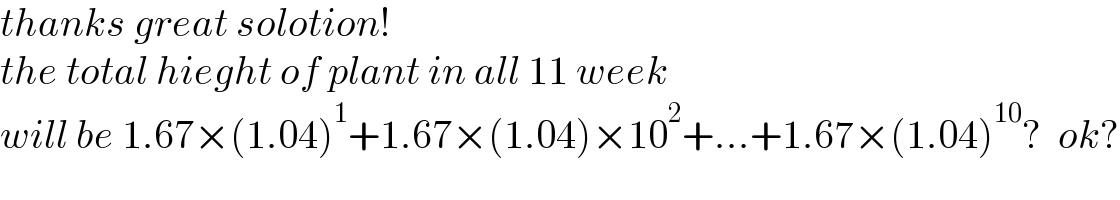
$${thanks}\:{great}\:{solotion}! \\ $$$${the}\:{total}\:{hieght}\:{of}\:{plant}\:{in}\:{all}\:\mathrm{11}\:{week} \\ $$$${will}\:{be}\:\mathrm{1}.\mathrm{67}×\left(\mathrm{1}.\mathrm{04}\right)^{\mathrm{1}} +\mathrm{1}.\mathrm{67}×\left(\mathrm{1}.\mathrm{04}\right)×\mathrm{10}^{\mathrm{2}} +…+\mathrm{1}.\mathrm{67}×\left(\mathrm{1}.\mathrm{04}\right)^{\mathrm{10}} ?\:\:{ok}? \\ $$
Answered by manxsol last updated on 25/May/23

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}{\mathrm{1}}&\hline{\mathrm{1}.\mathrm{67}×\mathrm{1}.\mathrm{04}^{\mathrm{0}} }\\{\mathrm{2}}&\hline{\mathrm{1}.\mathrm{67}×\mathrm{1}.\mathrm{04}^{\mathrm{1}} }\\{\mathrm{3}}&\hline{\mathrm{1}.\mathrm{67}×\mathrm{1}.\mathrm{04}^{\mathrm{2}} }\\{}&\hline{}\\{}&\hline{}\\{}&\hline{}\\{}&\hline{}\\{\mathrm{11}}&\hline{\mathrm{1}.\mathrm{67}×\mathrm{1}.\mathrm{04}^{\mathrm{10}} }\\{{n}}&\hline{\mathrm{1}.\mathrm{67}×\mathrm{1}.\mathrm{04}^{{n}−\mathrm{1}} }\\{\sum_{\mathrm{1}} ^{\mathrm{11}} }&\hline{\mathrm{1}.\mathrm{67}\:\left(\frac{\mathrm{1}.\mathrm{04}^{\mathrm{11}} −\mathrm{1}}{\mathrm{1}.\mathrm{04}−\mathrm{1}}\right)}\\\hline\end{array} \\ $$$$\mathrm{1}.\mathrm{67}\:\left(\frac{\mathrm{1}.\mathrm{04}^{\mathrm{11}} −\mathrm{1}}{\mathrm{1}.\mathrm{04}−\mathrm{1}}\right) \\ $$$$\mathrm{22}.\mathrm{522207} \\ $$$${n}=\mathrm{11} \\ $$$${r}=\mathrm{1}.\mathrm{04} \\ $$$${a}_{\mathrm{1}} =\mathrm{1}.\mathrm{67} \\ $$$$\Sigma{progresion}\:{geometric}= \\ $$$${a}_{\mathrm{1}} \frac{\left({r}^{{n}} −\mathrm{1}\right)}{{r}−\mathrm{1}} \\ $$$$ \\ $$
Commented by sciencestudentW last updated on 28/May/23

$${nice} \\ $$
