Question Number 61694 by naka3546 last updated on 06/Jun/19
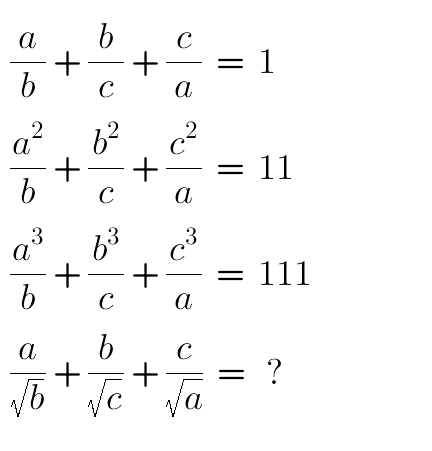
Commented by MJS last updated on 07/Jun/19
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this} \\ $$
Answered by ajfour last updated on 08/Jun/19
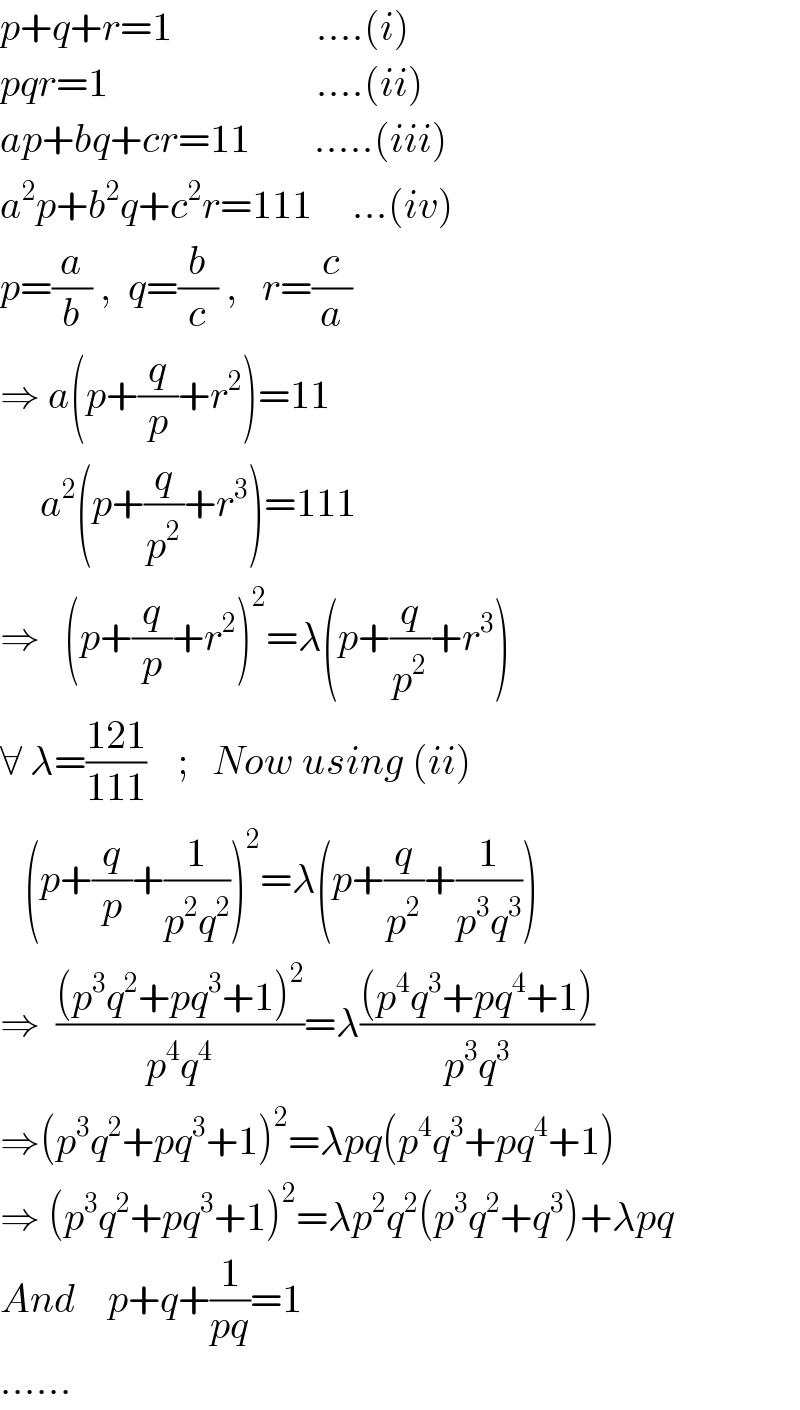
$${p}+{q}+{r}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({i}\right) \\ $$$${pqr}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$${ap}+{bq}+{cr}=\mathrm{11}\:\:\:\:\:\:\:\:…..\left({iii}\right) \\ $$$${a}^{\mathrm{2}} {p}+{b}^{\mathrm{2}} {q}+{c}^{\mathrm{2}} {r}=\mathrm{111}\:\:\:\:\:…\left({iv}\right) \\ $$$${p}=\frac{{a}}{{b}}\:,\:\:{q}=\frac{{b}}{{c}}\:,\:\:\:{r}=\frac{{c}}{{a}} \\ $$$$\Rightarrow\:{a}\left({p}+\frac{{q}}{{p}}+{r}^{\mathrm{2}} \right)=\mathrm{11} \\ $$$$\:\:\:\:\:{a}^{\mathrm{2}} \left({p}+\frac{{q}}{{p}^{\mathrm{2}} }+{r}^{\mathrm{3}} \right)=\mathrm{111} \\ $$$$\Rightarrow\:\:\:\left({p}+\frac{{q}}{{p}}+{r}^{\mathrm{2}} \right)^{\mathrm{2}} =\lambda\left({p}+\frac{{q}}{{p}^{\mathrm{2}} }+{r}^{\mathrm{3}} \right) \\ $$$$\forall\:\lambda=\frac{\mathrm{121}}{\mathrm{111}}\:\:\:\:;\:\:\:{Now}\:{using}\:\left({ii}\right) \\ $$$$\:\:\:\left({p}+\frac{{q}}{{p}}+\frac{\mathrm{1}}{{p}^{\mathrm{2}} {q}^{\mathrm{2}} }\right)^{\mathrm{2}} =\lambda\left({p}+\frac{{q}}{{p}^{\mathrm{2}} }+\frac{\mathrm{1}}{{p}^{\mathrm{3}} {q}^{\mathrm{3}} }\right) \\ $$$$\Rightarrow\:\:\frac{\left({p}^{\mathrm{3}} {q}^{\mathrm{2}} +{pq}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{{p}^{\mathrm{4}} {q}^{\mathrm{4}} }=\lambda\frac{\left({p}^{\mathrm{4}} {q}^{\mathrm{3}} +{pq}^{\mathrm{4}} +\mathrm{1}\right)}{{p}^{\mathrm{3}} {q}^{\mathrm{3}} } \\ $$$$\Rightarrow\left({p}^{\mathrm{3}} {q}^{\mathrm{2}} +{pq}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} =\lambda{pq}\left({p}^{\mathrm{4}} {q}^{\mathrm{3}} +{pq}^{\mathrm{4}} +\mathrm{1}\right) \\ $$$$\Rightarrow\:\left({p}^{\mathrm{3}} {q}^{\mathrm{2}} +{pq}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} =\lambda{p}^{\mathrm{2}} {q}^{\mathrm{2}} \left({p}^{\mathrm{3}} {q}^{\mathrm{2}} +{q}^{\mathrm{3}} \right)+\lambda{pq} \\ $$$${And}\:\:\:\:{p}+{q}+\frac{\mathrm{1}}{{pq}}=\mathrm{1} \\ $$$$…… \\ $$
