Question-61809

Question Number 61809 by aliesam last updated on 09/Jun/19

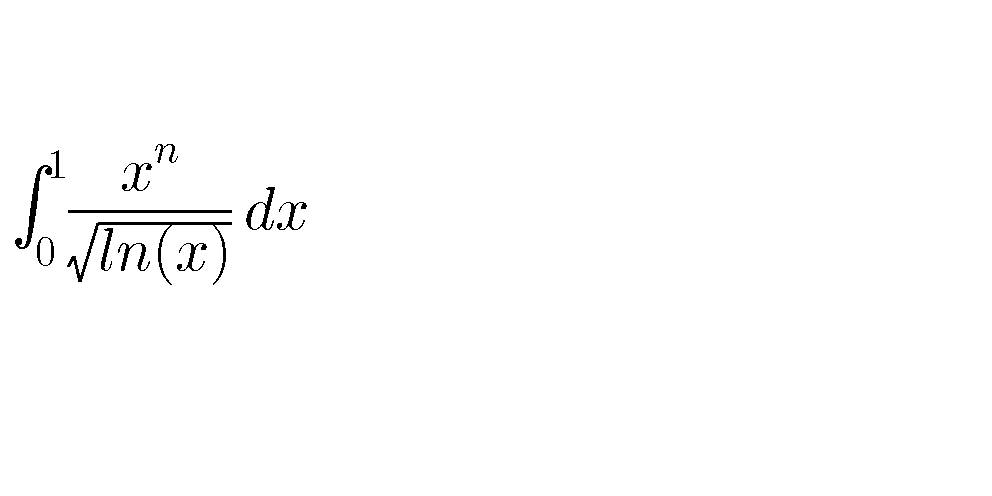
Commented by maxmathsup by imad last updated on 10/Jun/19

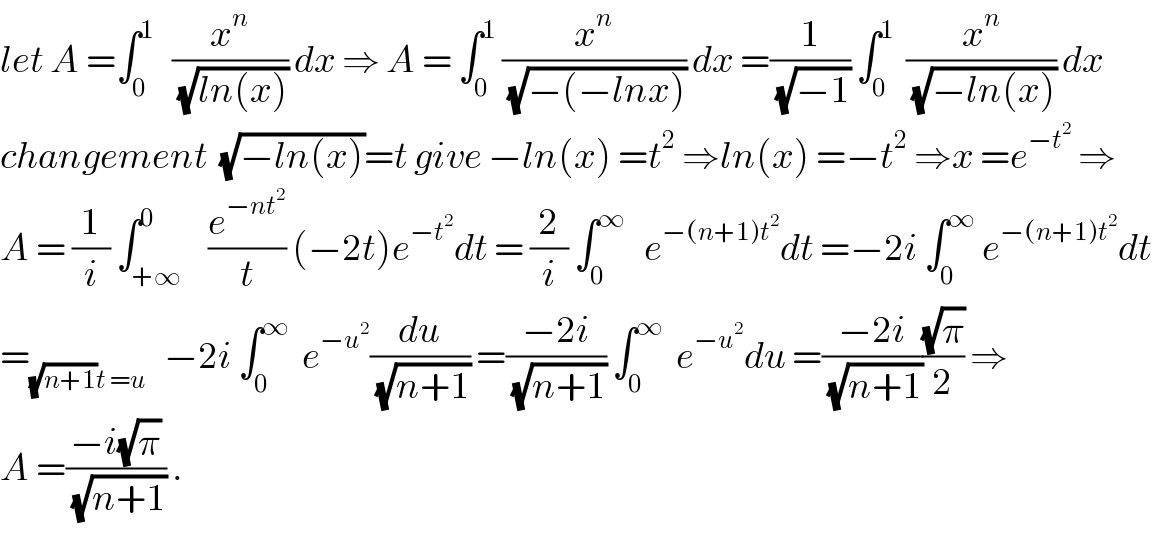
let A =∫_0 ^1 (x^n /( (√(ln(x))))) dx ⇒ A = ∫_0 ^1 (x^n /( (√(−(−lnx))))) dx =(1/( (√(−1)))) ∫_0 ^1 (x^n /( (√(−ln(x))))) dx changement (√(−ln(x)))=t give −ln(x) =t^2 ⇒ln(x) =−t^2 ⇒x =e^(−t^2 ) ⇒ A = (1/i) ∫_(+∞) ^0 (e^(−nt^2 ) /t) (−2t)e^(−t^2 ) dt = (2/i) ∫_0 ^∞ e^(−(n+1)t^2 ) dt =−2i ∫_0 ^∞ e^(−(n+1)t^2 ) dt =_((√(n+1))t =u) −2i ∫_0 ^∞ e^(−u^2 ) (du/( (√(n+1)))) =((−2i)/( (√(n+1)))) ∫_0 ^∞ e^(−u^2 ) du =((−2i)/( (√(n+1))))((√π)/2) ⇒ A =((−i(√π))/( (√(n+1)))) .

$${let}\:{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{{n}} }{\:\sqrt{{ln}\left({x}\right)}}\:{dx}\:\Rightarrow\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} }{\:\sqrt{−\left(−{lnx}\right)}}\:{dx}\:=\frac{\mathrm{1}}{\:\sqrt{−\mathrm{1}}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{x}^{{n}} }{\:\sqrt{−{ln}\left({x}\right)}}\:{dx} \\ $$$${changement}\:\:\sqrt{−{ln}\left({x}\right)}={t}\:{give}\:−{ln}\left({x}\right)\:={t}^{\mathrm{2}} \:\Rightarrow{ln}\left({x}\right)\:=−{t}^{\mathrm{2}} \:\Rightarrow{x}\:={e}^{−{t}^{\mathrm{2}} } \:\Rightarrow \\ $$$${A}\:=\:\frac{\mathrm{1}}{{i}}\:\int_{+\infty} ^{\mathrm{0}} \:\:\:\frac{{e}^{−{nt}^{\mathrm{2}} } }{{t}}\:\left(−\mathrm{2}{t}\right){e}^{−{t}^{\mathrm{2}} } {dt}\:=\:\frac{\mathrm{2}}{{i}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−\left({n}+\mathrm{1}\right){t}^{\mathrm{2}} } {dt}\:=−\mathrm{2}{i}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({n}+\mathrm{1}\right){t}^{\mathrm{2}} } {dt} \\ $$$$=_{\sqrt{{n}+\mathrm{1}}{t}\:={u}} \:\:\:−\mathrm{2}{i}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{u}^{\mathrm{2}} } \frac{{du}}{\:\sqrt{{n}+\mathrm{1}}}\:=\frac{−\mathrm{2}{i}}{\:\sqrt{{n}+\mathrm{1}}}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\:=\frac{−\mathrm{2}{i}}{\:\sqrt{{n}+\mathrm{1}}}\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow \\ $$$${A}\:=\frac{−{i}\sqrt{\pi}}{\:\sqrt{{n}+\mathrm{1}}}\:. \\ $$

Answered by perlman last updated on 09/Jun/19

(√(ln(x)))=i(√(−ln(x))) ∀x∈]0;1] withe (√(−ln(x)))=y x=e^(−y^2 ) =∫_(+∞) ^0 (e^(−ny^2 ) /(iy))(−2y)e^(−y^2 ) dy =i∫_0 ^(+∞) e^(−(n+1)y^2 ) dy let z=(√((n+1)))y dz=(√(n+1))dy =i∫_0 ^(+∞) (√(n+1))e^(−z^2 ) dz=i(√(n+1))∫_0 ^(+∞) e^(−z^2 ) dz=i(√(n+1))((√π)/2)

$$\left.\sqrt{{ln}\left({x}\right)}\left.={i}\sqrt{−{ln}\left({x}\right)}\:\:\forall{x}\in\right]\mathrm{0};\mathrm{1}\right] \\ $$$${withe}\:\sqrt{−{ln}\left({x}\right)}={y} \\ $$$${x}={e}^{−{y}^{\mathrm{2}} } \\ $$$$=\int_{+\infty} ^{\mathrm{0}} \frac{{e}^{−{ny}^{\mathrm{2}} } }{{iy}}\left(−\mathrm{2}{y}\right){e}^{−{y}^{\mathrm{2}} } {dy} \\ $$$$={i}\int_{\mathrm{0}} ^{+\infty} {e}^{−\left({n}+\mathrm{1}\right){y}^{\mathrm{2}} } {dy} \\ $$$${let}\:{z}=\sqrt{\left({n}+\mathrm{1}\right)}{y} \\ $$$${dz}=\sqrt{{n}+\mathrm{1}}{dy} \\ $$$$={i}\int_{\mathrm{0}} ^{+\infty} \sqrt{{n}+\mathrm{1}}{e}^{−\boldsymbol{{z}}^{\mathrm{2}} } \boldsymbol{{dz}}=\boldsymbol{{i}}\sqrt{\boldsymbol{{n}}+\mathrm{1}}\int_{\mathrm{0}} ^{+\infty} {e}^{−{z}^{\mathrm{2}} } {dz}={i}\sqrt{{n}+\mathrm{1}}\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply