Menu Close

advanced-calculus-prove-1023-134-0-x-2-5-x-2-5-1-x-2-1-1024x-2-dx-pi-golden-ratio-

Tinku Tara 0 Comments
Pin




Question Number 127370 by mnjuly1970 last updated on 29/Dec/20
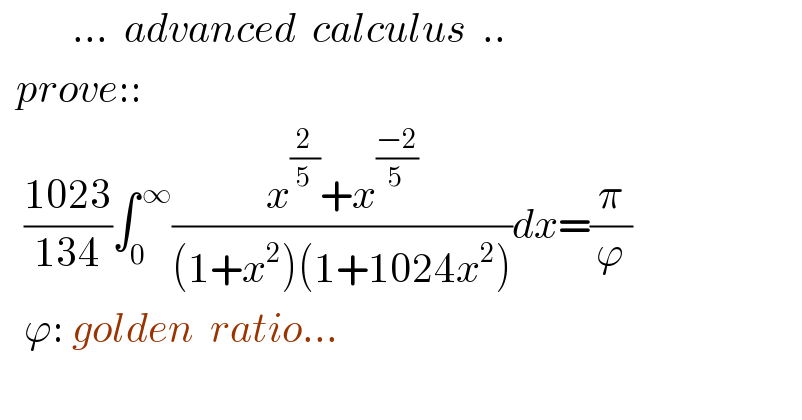
... advanced calculus .. prove:: ((1023)/(134))∫_0 ^( ∞) ((x^(2/5) +x^((−2)/5) )/((1+x^2 )(1+1024x^2 )))dx=(π/ϕ) ϕ: golden ratio...
$$\:\:\:\:\:\:\:\:\:…\:\:{advanced}\:\:{calculus}\:\:.. \\ $$$$\:\:{prove}:: \\ $$$$\:\:\:\frac{\mathrm{1023}}{\mathrm{134}}\int_{\mathrm{0}} ^{\:\infty} \frac{{x}^{\frac{\mathrm{2}}{\mathrm{5}}} +{x}^{\frac{−\mathrm{2}}{\mathrm{5}}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{1024}{x}^{\mathrm{2}} \right)}{dx}=\frac{\pi}{\varphi} \\ $$$$\:\:\:\varphi:\:{golden}\:\:{ratio}… \\ $$$$ \\ $$
Commented by liberty last updated on 29/Dec/20
inkjesti ta 'livell għoli. straordinarja
Answered by mindispower last updated on 29/Dec/20
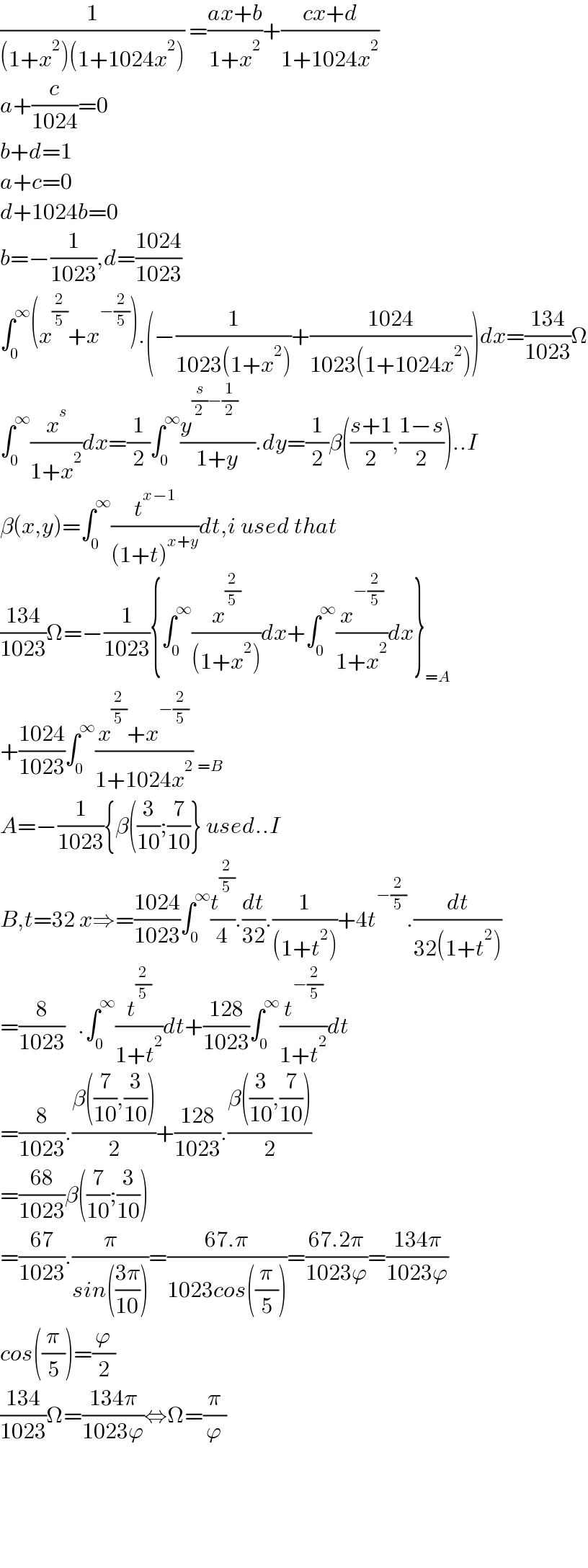
(1/((1+x^2 )(1+1024x^2 ))) =((ax+b)/(1+x^2 ))+((cx+d)/(1+1024x^2 )) a+(c/(1024))=0 b+d=1 a+c=0 d+1024b=0 b=−(1/(1023)),d=((1024)/(1023)) ∫_0 ^∞ (x^(2/5) +x^(−(2/5)) ).(−(1/(1023(1+x^2 )))+((1024)/(1023(1+1024x^2 ))))dx=((134)/(1023))Ω ∫_0 ^∞ (x^s /(1+x^2 ))dx=(1/2)∫_0 ^∞ ((y^((s/2)−(1/2)) )/(1+y)).dy=(1/2)β(((s+1)/2),((1−s)/2))..I β(x,y)=∫_0 ^∞ (t^(x−1) /((1+t)^(x+y) ))dt,i used that ((134)/(1023))Ω=−(1/(1023)){∫_0 ^∞ (x^(2/5) /((1+x^2 )))dx+∫_0 ^∞ (x^(−(2/5)) /(1+x^2 ))dx}_(=A) +((1024)/(1023))∫_0 ^∞ ((x^(2/5) +x^(−(2/5)) )/(1+1024x^2 )) _(=B) A=−(1/(1023)){β((3/(10));(7/(10))} used..I B,t=32 x⇒=((1024)/(1023))∫_0 ^∞ (t^(2/5) /4).(dt/(32)).(1/((1+t^2 )))+4t^(−(2/5)) .(dt/(32(1+t^2 ))) =(8/(1023)) .∫_0 ^∞ (t^(2/5) /(1+t^2 ))dt+((128)/(1023))∫_0 ^∞ (t^(−(2/5)) /(1+t^2 ))dt =(8/(1023)).((β((7/(10)),(3/(10))))/2)+((128)/(1023)).((β((3/(10)),(7/(10))))/2) =((68)/(1023))β((7/(10));(3/(10))) =((67)/(1023)).(π/(sin(((3π)/(10)))))=((67.π)/(1023cos((π/5))))=((67.2π)/(1023ϕ))=((134π)/(1023ϕ)) cos((π/5))=(ϕ/2) ((134)/(1023))Ω=((134π)/(1023ϕ))⇔Ω=(π/ϕ)
$$\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+\mathrm{1024}{x}^{\mathrm{2}} \right)}\:=\frac{{ax}+{b}}{\mathrm{1}+{x}^{\mathrm{2}} }+\frac{{cx}+{d}}{\mathrm{1}+\mathrm{1024}{x}^{\mathrm{2}} } \\ $$$${a}+\frac{{c}}{\mathrm{1024}}=\mathrm{0} \\ $$$${b}+{d}=\mathrm{1} \\ $$$${a}+{c}=\mathrm{0} \\ $$$${d}+\mathrm{1024}{b}=\mathrm{0} \\ $$$${b}=−\frac{\mathrm{1}}{\mathrm{1023}},{d}=\frac{\mathrm{1024}}{\mathrm{1023}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \left({x}^{\frac{\mathrm{2}}{\mathrm{5}}} +{x}^{−\frac{\mathrm{2}}{\mathrm{5}}} \right).\left(−\frac{\mathrm{1}}{\mathrm{1023}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}+\frac{\mathrm{1024}}{\mathrm{1023}\left(\mathrm{1}+\mathrm{1024}{x}^{\mathrm{2}} \right)}\right){dx}=\frac{\mathrm{134}}{\mathrm{1023}}\Omega \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{s}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{y}^{\frac{{s}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\:}{\mathrm{1}+{y}}.{dy}=\frac{\mathrm{1}}{\mathrm{2}}\beta\left(\frac{{s}+\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}−{s}}{\mathrm{2}}\right)..{I} \\ $$$$\beta\left({x},{y}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{x}−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{{x}+{y}} }{dt},{i}\:{used}\:{that} \\ $$$$\frac{\mathrm{134}}{\mathrm{1023}}\Omega=−\frac{\mathrm{1}}{\mathrm{1023}}\left\{\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\mathrm{2}}{\mathrm{5}}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{0}} ^{\infty} \frac{{x}^{−\frac{\mathrm{2}}{\mathrm{5}}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right\}_{={A}} \\ $$$$+\frac{\mathrm{1024}}{\mathrm{1023}}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\mathrm{2}}{\mathrm{5}}} +{x}^{−\frac{\mathrm{2}}{\mathrm{5}}} }{\mathrm{1}+\mathrm{1024}{x}^{\mathrm{2}} }\:_{={B}} \\ $$$${A}=−\frac{\mathrm{1}}{\mathrm{1023}}\left\{\beta\left(\frac{\mathrm{3}}{\mathrm{10}};\frac{\mathrm{7}}{\mathrm{10}}\right\}\:{used}..{I}\right. \\ $$$${B},{t}=\mathrm{32}\:{x}\Rightarrow=\frac{\mathrm{1024}}{\mathrm{1023}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{\mathrm{2}}{\mathrm{5}}} }{\mathrm{4}}.\frac{{dt}}{\mathrm{32}}.\frac{\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}+\mathrm{4}{t}^{−\frac{\mathrm{2}}{\mathrm{5}}} .\frac{{dt}}{\mathrm{32}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{8}}{\mathrm{1023}}\:\:\:.\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{\mathrm{2}}{\mathrm{5}}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt}+\frac{\mathrm{128}}{\mathrm{1023}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{−\frac{\mathrm{2}}{\mathrm{5}}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{8}}{\mathrm{1023}}.\frac{\beta\left(\frac{\mathrm{7}}{\mathrm{10}},\frac{\mathrm{3}}{\mathrm{10}}\right)}{\mathrm{2}}+\frac{\mathrm{128}}{\mathrm{1023}}.\frac{\beta\left(\frac{\mathrm{3}}{\mathrm{10}},\frac{\mathrm{7}}{\mathrm{10}}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{68}}{\mathrm{1023}}\beta\left(\frac{\mathrm{7}}{\mathrm{10}};\frac{\mathrm{3}}{\mathrm{10}}\right) \\ $$$$=\frac{\mathrm{67}}{\mathrm{1023}}.\frac{\pi}{{sin}\left(\frac{\mathrm{3}\pi}{\mathrm{10}}\right)}=\frac{\mathrm{67}.\pi}{\mathrm{1023}{cos}\left(\frac{\pi}{\mathrm{5}}\right)}=\frac{\mathrm{67}.\mathrm{2}\pi}{\mathrm{1023}\varphi}=\frac{\mathrm{134}\pi}{\mathrm{1023}\varphi} \\ $$$${cos}\left(\frac{\pi}{\mathrm{5}}\right)=\frac{\varphi}{\mathrm{2}} \\ $$$$\frac{\mathrm{134}}{\mathrm{1023}}\Omega=\frac{\mathrm{134}\pi}{\mathrm{1023}\varphi}\Leftrightarrow\Omega=\frac{\pi}{\varphi} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 29/Dec/20
thanks alot sir power very nice as always.. grateful..
$${thanks}\:{alot}\:{sir}\:{power}\: \\ $$$$\:{very}\:{nice}\:{as}\:{always}.. \\ $$$${grateful}.. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *