Menu Close

let-V-be-a-vector-space-and-let-H-and-K-be-subspace-of-V-show-that-H-K-x-x-h-k-where-h-H-and-k-K-is-a-subspace-of-V-

Tinku Tara 0 Comments
Pin




Question Number 61843 by psyche last updated on 10/Jun/19
let V be a vector space and let H and K be subspace of V. show that , H+K={x:x=h+k, where h∈H and k∈K} is a subspace of V.
$$\boldsymbol{{let}}\:\boldsymbol{{V}}\:\:\:\boldsymbol{{be}}\:\boldsymbol{{a}}\:\boldsymbol{{vector}}\:\boldsymbol{{space}}\:\boldsymbol{{and}}\:\boldsymbol{{let}}\:\boldsymbol{{H}}\:\boldsymbol{{and}}\:\boldsymbol{{K}}\:\boldsymbol{{be}}\: \\ $$$$\boldsymbol{{subspace}}\:\boldsymbol{{of}}\:\boldsymbol{{V}}.\:\boldsymbol{{show}}\:\boldsymbol{{that}}\:, \\ $$$${H}+{K}=\left\{\boldsymbol{{x}}:\boldsymbol{{x}}=\boldsymbol{{h}}+\boldsymbol{{k}},\:\boldsymbol{{where}}\:\boldsymbol{{h}}\in{H}\:\boldsymbol{{and}}\:\:\boldsymbol{{k}}\in{K}\right\}\:\boldsymbol{{is}}\:\:\boldsymbol{{a}}\:\boldsymbol{{subspace}}\:\boldsymbol{{of}}\:\boldsymbol{{V}}.\: \\ $$
Commented by arcana last updated on 10/Jun/19
if V is a vector space over a field K. • H+K is a nonempty subset,0∈H+K • x∈H+K, x=h+k, h∈H,k∈K, where H⊆V,K⊆V ⇒x=h+k∈V. H+K⊆V •if x=h_1 +k_1 ,y=h_2 +k_2 ,h_1 ,h_2 ∈H,k_1 ,k_2 ∈K x+y=(h_1 +k_1 )+(h_2 +k_2 )=(h_1 +h_2 )+(k_1 +k_2 ), V group abelian under “+” =h+k with h=h_1 +h_2 ∈H,k=k_1 +k_2 ∈K ⇒x+y∈H+K • if a∈K,x=h+k∈H+K.a∙x=a(h+k) =a∙h+a∙k. H and K are subspaces⇒a∙h∈H,a∙k∈K ⇒a∙x∈H+K
$$\mathrm{if}\:\mathrm{V}\:\mathrm{is}\:\mathrm{a}\:\mathrm{vector}\:\mathrm{space}\:\mathrm{over}\:\mathrm{a}\:\mathrm{field}\:\mathrm{K}. \\ $$$$\bullet\:\mathrm{H}+\mathrm{K}\:\mathrm{is}\:\mathrm{a}\:\mathrm{nonempty}\:\mathrm{subset},\mathrm{0}\in\mathrm{H}+\mathrm{K} \\ $$$$ \\ $$$$\bullet\:{x}\in\mathrm{H}+\mathrm{K},\:{x}={h}+{k},\:{h}\in\mathrm{H},{k}\in\mathrm{K},\:\mathrm{where} \\ $$$$\mathrm{H}\subseteq\mathrm{V},\mathrm{K}\subseteq\mathrm{V}\:\Rightarrow{x}={h}+{k}\in\mathrm{V}.\:\mathrm{H}+\mathrm{K}\subseteq\mathrm{V} \\ $$$$ \\ $$$$\bullet\mathrm{if}\:{x}={h}_{\mathrm{1}} +{k}_{\mathrm{1}} ,{y}={h}_{\mathrm{2}} +{k}_{\mathrm{2}} ,{h}_{\mathrm{1}} ,{h}_{\mathrm{2}} \in\mathrm{H},{k}_{\mathrm{1}} ,{k}_{\mathrm{2}} \in\mathrm{K} \\ $$$${x}+{y}=\left({h}_{\mathrm{1}} +{k}_{\mathrm{1}} \right)+\left({h}_{\mathrm{2}} +{k}_{\mathrm{2}} \right)=\left({h}_{\mathrm{1}} +{h}_{\mathrm{2}} \right)+\left({k}_{\mathrm{1}} +{k}_{\mathrm{2}} \right),\:\mathrm{V}\:\mathrm{group}\:\mathrm{abelian}\:\mathrm{under}\:“+'' \\ $$$$={h}+{k}\:\mathrm{with}\:{h}={h}_{\mathrm{1}} +{h}_{\mathrm{2}} \in\mathrm{H},{k}={k}_{\mathrm{1}} +{k}_{\mathrm{2}} \in\mathrm{K} \\ $$$$\Rightarrow{x}+{y}\in\mathrm{H}+\mathrm{K} \\ $$$$ \\ $$$$\bullet\:\mathrm{if}\:{a}\in\mathrm{K},{x}={h}+{k}\in\mathrm{H}+\mathrm{K}.{a}\centerdot{x}={a}\left({h}+{k}\right) \\ $$$$={a}\centerdot{h}+{a}\centerdot{k}.\:{H}\:\mathrm{and}\:\mathrm{K}\:\mathrm{are}\:\mathrm{subspace}{s}\Rightarrow{a}\centerdot{h}\in\mathrm{H},{a}\centerdot{k}\in\mathrm{K} \\ $$$$\Rightarrow{a}\centerdot{x}\in\mathrm{H}+\mathrm{K} \\ $$$$ \\ $$
Commented by arcana last updated on 10/Jun/19
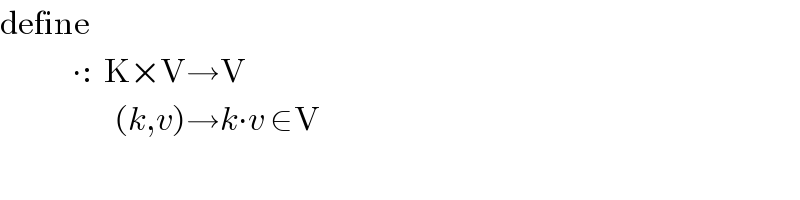
define ∙: K×V→V (k,v)→k∙v ∈V
$$\mathrm{define}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\centerdot:\:\:\mathrm{K}×\mathrm{V}\rightarrow\mathrm{V} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({k},{v}\right)\rightarrow{k}\centerdot{v}\:\in\mathrm{V} \\ $$
Commented by arcana last updated on 10/Jun/19
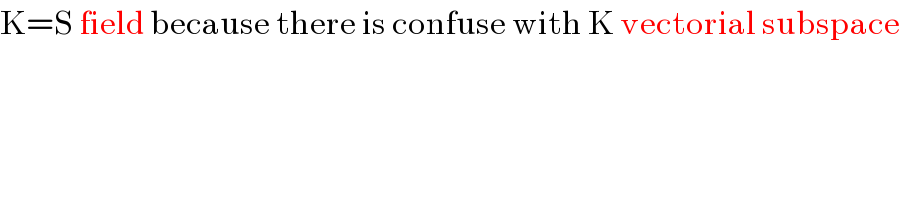
K=S field because there is confuse with K vectorial subspace
$$\mathrm{K}=\mathrm{S}\:\mathrm{field}\:\mathrm{because}\:\mathrm{there}\:\mathrm{is}\:\mathrm{confuse}\:\mathrm{with}\:\mathrm{K}\:\mathrm{vectorial}\:\mathrm{subspace} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *