Question Number 62185 by aliesam last updated on 17/Jun/19
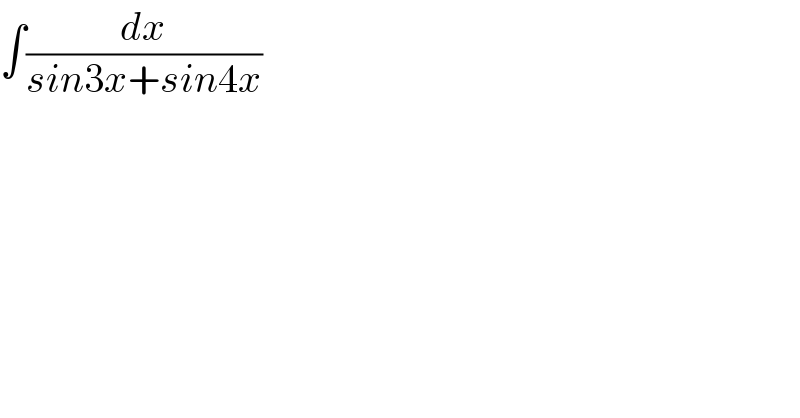
$$\int\frac{{dx}}{{sin}\mathrm{3}{x}+{sin}\mathrm{4}{x}} \\ $$
Answered by MJS last updated on 17/Jun/19
![∫(dx/(sin 3x +sin 4x))= [t=(1/(cos x)) → dx=((cos^2 x)/(sin x))] =−∫(t^3 /((t−1)(t+1)(t^3 +4t^2 −4t−8)))dt= [((α=−(4/3)(1−(√7)sin ((1/3)arcsin ((√7)/(14)))))),((β=(4/3)(−1+(√7)cos ((π/6)+arcsin ((√7)/(14)))))),((γ=−(4/3)(1+(√7)sin ((π/3)+arcsin ((√7)/(14)))))) ] =−∫(t^3 /((t−1)(t+1)(t−α)(t−β)(t−γ)))dt= =(1/(14))∫(dt/(t−1))+(1/2)∫(dt/(t+1))+(γ/7)∫(dt/(t−α))+(α/7)∫(dt/(t−β))+(β/7)∫(dt/(t−γ))= =(1/(14))ln (t−1) +(1/2)ln (t+1) +(γ/7)ln (t−α) +(α/7)ln (t−β) +(β/7)ln (t−γ) now put t=(1/(cos x)) ⇒ it′s easy to solve but hard to write out [and it was not easy to find the constants]](https://www.tinkutara.com/question/Q62212.png)
$$\int\frac{{dx}}{\mathrm{sin}\:\mathrm{3}{x}\:+\mathrm{sin}\:\mathrm{4}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{1}}{\mathrm{cos}\:{x}}\:\rightarrow\:{dx}=\frac{\mathrm{cos}^{\mathrm{2}} \:{x}}{\mathrm{sin}\:{x}}\right] \\ $$$$=−\int\frac{{t}^{\mathrm{3}} }{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{3}} +\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{t}−\mathrm{8}\right)}{dt}= \\ $$$$\:\:\:\:\:\begin{bmatrix}{\alpha=−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{1}−\sqrt{\mathrm{7}}\mathrm{sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\right)}\\{\beta=\frac{\mathrm{4}}{\mathrm{3}}\left(−\mathrm{1}+\sqrt{\mathrm{7}}\mathrm{cos}\:\left(\frac{\pi}{\mathrm{6}}+\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\right)}\\{\gamma=−\frac{\mathrm{4}}{\mathrm{3}}\left(\mathrm{1}+\sqrt{\mathrm{7}}\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\mathrm{arcsin}\:\frac{\sqrt{\mathrm{7}}}{\mathrm{14}}\right)\right)}\end{bmatrix} \\ $$$$=−\int\frac{{t}^{\mathrm{3}} }{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}−\alpha\right)\left({t}−\beta\right)\left({t}−\gamma\right)}{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{14}}\int\frac{{dt}}{{t}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}+\mathrm{1}}+\frac{\gamma}{\mathrm{7}}\int\frac{{dt}}{{t}−\alpha}+\frac{\alpha}{\mathrm{7}}\int\frac{{dt}}{{t}−\beta}+\frac{\beta}{\mathrm{7}}\int\frac{{dt}}{{t}−\gamma}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{14}}\mathrm{ln}\:\left({t}−\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:+\frac{\gamma}{\mathrm{7}}\mathrm{ln}\:\left({t}−\alpha\right)\:+\frac{\alpha}{\mathrm{7}}\mathrm{ln}\:\left({t}−\beta\right)\:+\frac{\beta}{\mathrm{7}}\mathrm{ln}\:\left({t}−\gamma\right) \\ $$$$\mathrm{now}\:\mathrm{put}\:{t}=\frac{\mathrm{1}}{\mathrm{cos}\:{x}} \\ $$$$\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{but}\:\mathrm{hard}\:\mathrm{to}\:\mathrm{write}\:\mathrm{out}\:\left[\mathrm{and}\right. \\ $$$$\left.\mathrm{it}\:\mathrm{was}\:\mathrm{not}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{constants}\right] \\ $$
Commented by aliesam last updated on 17/Jun/19

$${thank}\:{yoy}\:{sir}\: \\ $$$${god}\:{bless}\:{you} \\ $$
Commented by MJS last updated on 17/Jun/19

$$\mathrm{I}\:\mathrm{tried}\:\mathrm{some}\:\mathrm{other}\:\mathrm{paths}\:\mathrm{but}\:\mathrm{none}\:\mathrm{worked}… \\ $$
Commented by aliesam last updated on 17/Jun/19
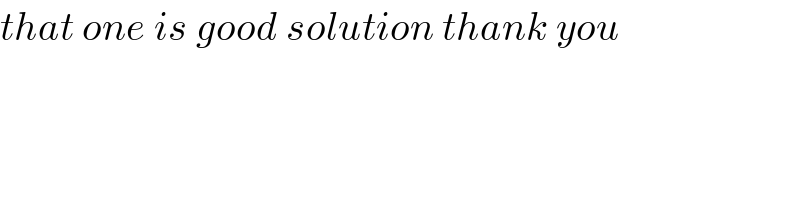
$${that}\:{one}\:{is}\:{good}\:{solution}\:{thank}\:{you} \\ $$
Commented by malwaan last updated on 18/Jun/19

$${GREAT}\:\:\:{SIR}\:{MJS} \\ $$$${thank}\:{you}\:{so}\:{much} \\ $$
