Menu Close

nice-calculus-if-b-gt-a-gt-0-then-prove-a-b-2-gt-b-a-ln-b-ln-a-gt-ab-

Tinku Tara 0 Comments
Pin




Question Number 128005 by mnjuly1970 last updated on 03/Jan/21
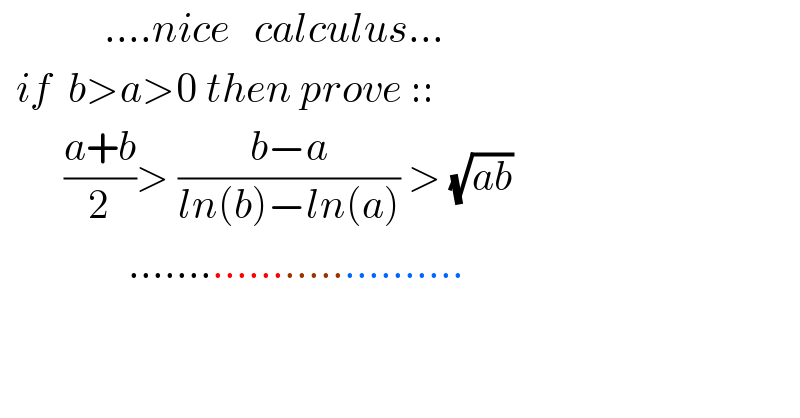
....nice calculus... if b>a>0 then prove :: ((a+b)/2)> ((b−a)/(ln(b)−ln(a))) > (√(ab)) ............................
$$\:\:\:\:\:\:\:\:\:\:\:\:\:….{nice}\:\:\:{calculus}… \\ $$$$\:\:{if}\:\:{b}>{a}>\mathrm{0}\:{then}\:{prove}\::: \\ $$$$\:\:\:\:\:\:\:\:\frac{{a}+{b}}{\mathrm{2}}>\:\frac{{b}−{a}}{{ln}\left({b}\right)−{ln}\left({a}\right)}\:>\:\sqrt{{ab}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………………………. \\ $$
Answered by mindispower last updated on 06/Jan/21
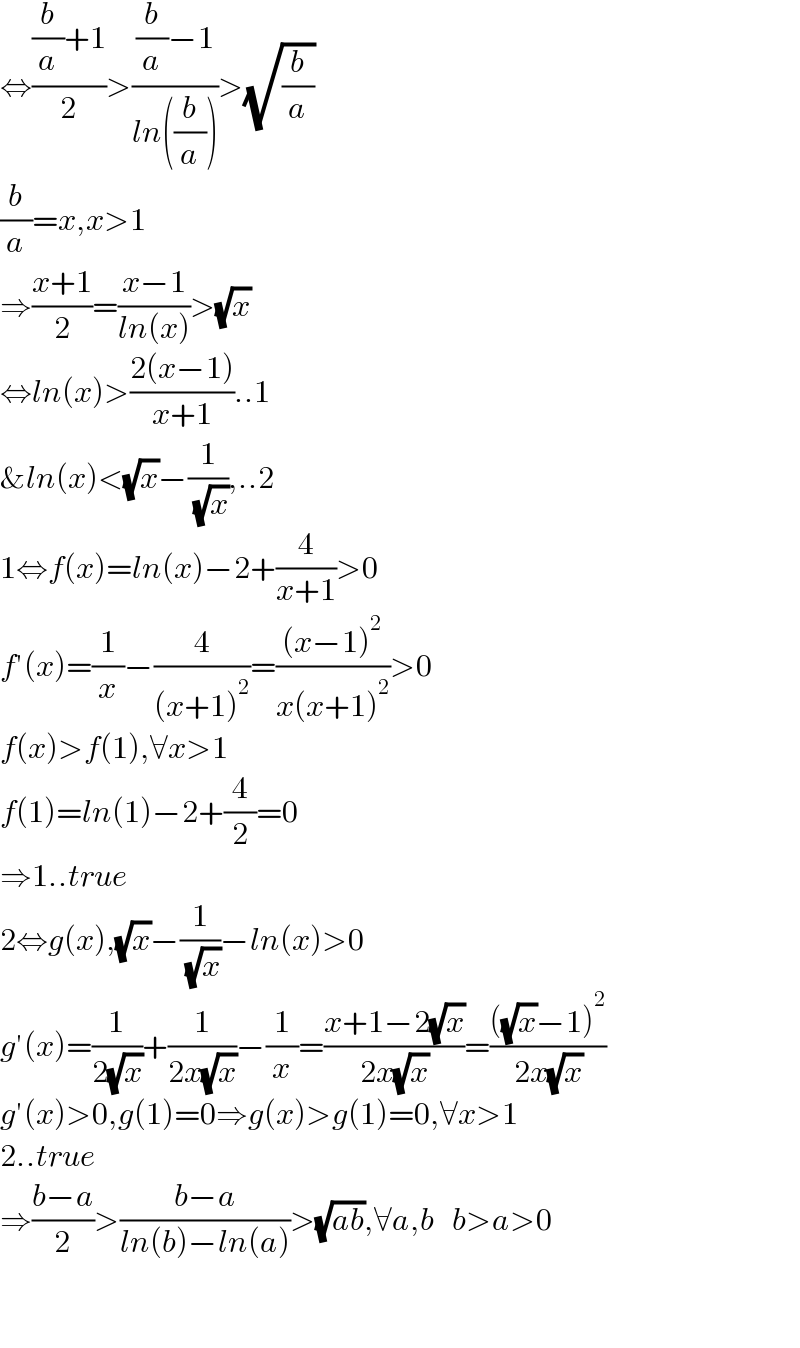
⇔(((b/a)+1)/2)>(((b/a)−1)/(ln((b/a))))>(√(b/a)) (b/a)=x,x>1 ⇒((x+1)/2)=((x−1)/(ln(x)))>(√x) ⇔ln(x)>((2(x−1))/(x+1))..1 &ln(x)<(√x)−(1/( (√x))),..2 1⇔f(x)=ln(x)−2+(4/(x+1))>0 f′(x)=(1/x)−(4/((x+1)^2 ))=(((x−1)^2 )/(x(x+1)^2 ))>0 f(x)>f(1),∀x>1 f(1)=ln(1)−2+(4/2)=0 ⇒1..true 2⇔g(x),(√x)−(1/( (√x)))−ln(x)>0 g′(x)=(1/(2(√x)))+(1/(2x(√x)))−(1/x)=((x+1−2(√x))/(2x(√x)))=((((√x)−1)^2 )/(2x(√x))) g′(x)>0,g(1)=0⇒g(x)>g(1)=0,∀x>1 2..true ⇒((b−a)/2)>((b−a)/(ln(b)−ln(a)))>(√(ab)),∀a,b b>a>0
$$\Leftrightarrow\frac{\frac{{b}}{{a}}+\mathrm{1}}{\mathrm{2}}>\frac{\frac{{b}}{{a}}−\mathrm{1}}{{ln}\left(\frac{{b}}{{a}}\right)}>\sqrt{\frac{{b}}{{a}}} \\ $$$$\frac{{b}}{{a}}={x},{x}>\mathrm{1} \\ $$$$\Rightarrow\frac{{x}+\mathrm{1}}{\mathrm{2}}=\frac{{x}−\mathrm{1}}{{ln}\left({x}\right)}>\sqrt{{x}} \\ $$$$\Leftrightarrow{ln}\left({x}\right)>\frac{\mathrm{2}\left({x}−\mathrm{1}\right)}{{x}+\mathrm{1}}..\mathrm{1} \\ $$$$\&{ln}\left({x}\right)<\sqrt{{x}}−\frac{\mathrm{1}}{\:\sqrt{{x}}},..\mathrm{2} \\ $$$$\mathrm{1}\Leftrightarrow{f}\left({x}\right)={ln}\left({x}\right)−\mathrm{2}+\frac{\mathrm{4}}{{x}+\mathrm{1}}>\mathrm{0} \\ $$$${f}'\left({x}\right)=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{4}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }>\mathrm{0} \\ $$$${f}\left({x}\right)>{f}\left(\mathrm{1}\right),\forall{x}>\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)={ln}\left(\mathrm{1}\right)−\mathrm{2}+\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}..{true} \\ $$$$\mathrm{2}\Leftrightarrow{g}\left({x}\right),\sqrt{{x}}−\frac{\mathrm{1}}{\:\sqrt{{x}}}−{ln}\left({x}\right)>\mathrm{0} \\ $$$${g}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}+\frac{\mathrm{1}}{\mathrm{2}{x}\sqrt{{x}}}−\frac{\mathrm{1}}{{x}}=\frac{{x}+\mathrm{1}−\mathrm{2}\sqrt{{x}}}{\mathrm{2}{x}\sqrt{{x}}}=\frac{\left(\sqrt{{x}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}{x}\sqrt{{x}}} \\ $$$${g}'\left({x}\right)>\mathrm{0},{g}\left(\mathrm{1}\right)=\mathrm{0}\Rightarrow{g}\left({x}\right)>{g}\left(\mathrm{1}\right)=\mathrm{0},\forall{x}>\mathrm{1} \\ $$$$\mathrm{2}..{true} \\ $$$$\Rightarrow\frac{{b}−{a}}{\mathrm{2}}>\frac{{b}−{a}}{{ln}\left({b}\right)−{ln}\left({a}\right)}>\sqrt{{ab}},\forall{a},{b}\:\:\:{b}>{a}>\mathrm{0} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *