Question-62577

Question Number 62577 by Sr@2004 last updated on 23/Jun/19

Commented by Sr@2004 last updated on 23/Jun/19

$${please}\:{solve}\:\mathrm{12} \\ $$

Answered by som(math1967) last updated on 23/Jun/19

(cscx−csczcscy)^2 =cot^2 ycot^2 z★ csc^2 x+csc^2 zcsc^2 y−2cscxcscycscz=(csc^2 y−1)cot^2 z csc^2 x+csc^2 y(1+cot^2 z)−2cscxcscycscz =cot^2 ycsc^2 z−cot^2 z csc^2 x+csc^2 y−2cscxcscycscz=−cot^2 z csc^2 x+csc^2 xcot^2 z+csc^2 y−2cscxcscycscz =−cot^2 z+csc^2 xcot^2 z★★ csc^2 x(1+cot^2 z) +csc^2 y−2cscycsczcscx =cot^2 z(csc^2 x−1) csc^2 xcsc^2 z+csc^2 y−2cscycscxcscz=cot^2 zcot^2 x (cscy−cscxcscz)^2 =cot^2 zcot^2 x (cscy−cscxcscz)=±cotzcotx ∴cosecy=cosecxcosecz±cotzcotx ★csc cosec ★★add cosec^2 xcot^2 z both side

$$\left({cscx}−{csczcscy}\right)^{\mathrm{2}} ={cot}^{\mathrm{2}} {ycot}^{\mathrm{2}} {z}\bigstar \\ $$$${csc}^{\mathrm{2}} {x}+{csc}^{\mathrm{2}} {zcsc}^{\mathrm{2}} {y}−\mathrm{2}{cscxcscycscz}=\left({csc}^{\mathrm{2}} {y}−\mathrm{1}\right){cot}^{\mathrm{2}} {z} \\ $$$${csc}^{\mathrm{2}} {x}+{csc}^{\mathrm{2}} {y}\left(\mathrm{1}+{cot}^{\mathrm{2}} {z}\right)−\mathrm{2}{cscxcscycscz} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={cot}^{\mathrm{2}} {ycsc}^{\mathrm{2}} {z}−{cot}^{\mathrm{2}} {z} \\ $$$${csc}^{\mathrm{2}} {x}+{csc}^{\mathrm{2}} {y}−\mathrm{2}{cscxcscycscz}=−{cot}^{\mathrm{2}} {z} \\ $$$${csc}^{\mathrm{2}} {x}+{csc}^{\mathrm{2}} {xcot}^{\mathrm{2}} {z}+{csc}^{\mathrm{2}} {y}−\mathrm{2}{cscxcscycscz} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−{cot}^{\mathrm{2}} {z}+{csc}^{\mathrm{2}} {xcot}^{\mathrm{2}} {z}\bigstar\bigstar \\ $$$${csc}^{\mathrm{2}} {x}\left(\mathrm{1}+{cot}^{\mathrm{2}} {z}\right)\:+{csc}^{\mathrm{2}} {y}−\mathrm{2}{cscycsczcscx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={cot}^{\mathrm{2}} {z}\left({csc}^{\mathrm{2}} {x}−\mathrm{1}\right) \\ $$$${csc}^{\mathrm{2}} {xcsc}^{\mathrm{2}} {z}+{csc}^{\mathrm{2}} {y}−\mathrm{2}{cscycscxcscz}={cot}^{\mathrm{2}} {zcot}^{\mathrm{2}} {x} \\ $$$$\left({cscy}−{cscxcscz}\right)^{\mathrm{2}} ={cot}^{\mathrm{2}} {zcot}^{\mathrm{2}} {x} \\ $$$$\left({cscy}−{cscxcscz}\right)=\pm{cotzcotx} \\ $$$$\therefore{cosecy}={cosecxcosecz}\pm{cotzcotx} \\ $$$$\bigstar{csc}\:\:{cosec} \\ $$$$\bigstar\bigstar{add}\:{cosec}^{\mathrm{2}} {xcot}^{\mathrm{2}} {z}\:{both}\:{side} \\ $$$$ \\ $$

Commented by Sr@2004 last updated on 24/Jun/19

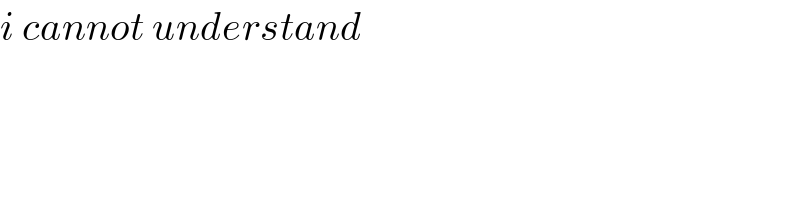
$${i}\:{cannot}\:{understand} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by som(math1967) last updated on 24/Jun/19

$${which}\:{line}? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply