Question Number 137277 by mnjuly1970 last updated on 31/Mar/21
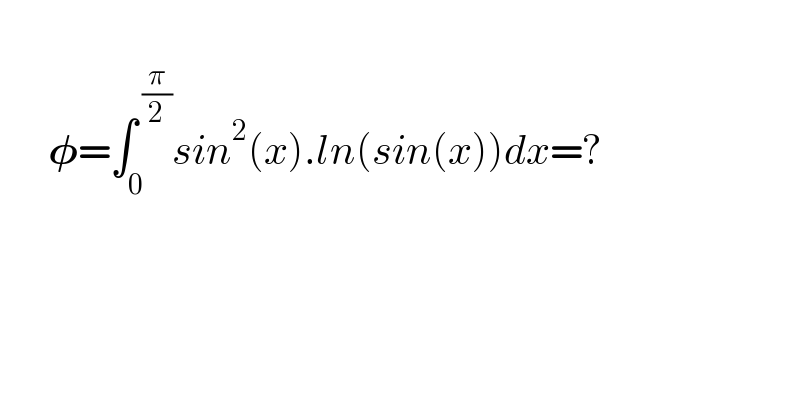
$$ \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} \left({x}\right).{ln}\left({sin}\left({x}\right)\right){dx}=? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 31/Mar/21
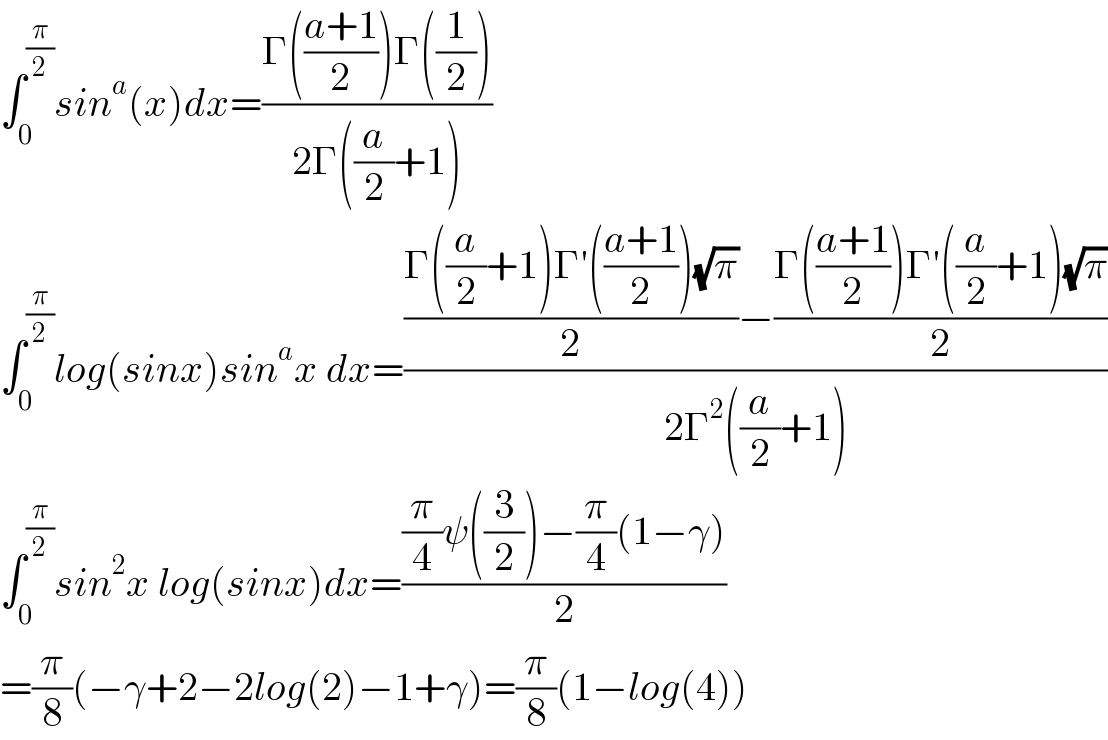
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{{a}} \left({x}\right){dx}=\frac{\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sinx}\right){sin}^{{a}} {x}\:{dx}=\frac{\frac{\Gamma\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)\Gamma'\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)\sqrt{\pi}}{\mathrm{2}}−\frac{\Gamma\left(\frac{{a}+\mathrm{1}}{\mathrm{2}}\right)\Gamma'\left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)\sqrt{\pi}}{\mathrm{2}}}{\mathrm{2}\Gamma^{\mathrm{2}} \left(\frac{{a}}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{\mathrm{2}} {x}\:{log}\left({sinx}\right){dx}=\frac{\frac{\pi}{\mathrm{4}}\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}}\left(\mathrm{1}−\gamma\right)}{\mathrm{2}} \\ $$$$=\frac{\pi}{\mathrm{8}}\left(−\gamma+\mathrm{2}−\mathrm{2}{log}\left(\mathrm{2}\right)−\mathrm{1}+\gamma\right)=\frac{\pi}{\mathrm{8}}\left(\mathrm{1}−{log}\left(\mathrm{4}\right)\right) \\ $$
Commented by mnjuly1970 last updated on 31/Mar/21
$$\:{very}\:{nice}.. \\ $$$${thank}\:{you}\:{mr}\:{Dwaipayan}.. \\ $$
Answered by Ar Brandon last updated on 31/Mar/21
![φ=∫_0 ^(π/2) sin^2 (x)ln(sinx)dx =(∂/∂α)∣_(α=2) ∫_0 ^(π/2) sin^α (x)dx=(∂/∂α)∣_(α=2) ((Γ(((α+1)/2))Γ((1/2)))/(2Γ(((α+2)/2)))) =((√π)/2)∣_(α=2) ((Γ((α/2)+1)Γ′((α/2)+(1/2))−Γ((α/2)+(1/2))Γ′((α/2)+1))/(Γ^2 ((α/2)+1))) =((√π)/2)∙(1/2)∙((Γ(2)Γ((3/2))[ψ((3/2))−ψ(2)])/(Γ^2 (2))) =(π/8)(2−γ−2ln2−1+γ)=(π/( 8))(1−2ln2)](https://www.tinkutara.com/question/Q137293.png)
$$\phi=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{sinx}\right)\mathrm{dx} \\ $$$$\:\:\:=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\alpha} \left(\mathrm{x}\right)\mathrm{dx}=\frac{\partial}{\partial\alpha}\mid_{\alpha=\mathrm{2}} \frac{\Gamma\left(\frac{\alpha+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\frac{\alpha+\mathrm{2}}{\mathrm{2}}\right)} \\ $$$$\:\:\:=\frac{\sqrt{\pi}}{\mathrm{2}}\mid_{\alpha=\mathrm{2}} \frac{\Gamma\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)\Gamma'\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\Gamma\left(\frac{\alpha}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma'\left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)}{\Gamma^{\mathrm{2}} \left(\frac{\alpha}{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$\:\:\:=\frac{\sqrt{\pi}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\Gamma\left(\mathrm{2}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\left[\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\mathrm{2}\right)\right]}{\Gamma^{\mathrm{2}} \left(\mathrm{2}\right)} \\ $$$$\:\:\:=\frac{\pi}{\mathrm{8}}\left(\mathrm{2}−\gamma−\mathrm{2ln2}−\mathrm{1}+\gamma\right)=\frac{\pi}{\:\mathrm{8}}\left(\mathrm{1}−\mathrm{2ln2}\right) \\ $$
Answered by Ñï= last updated on 31/Mar/21
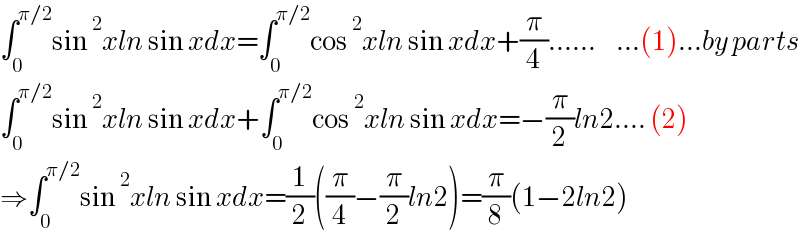
$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {xln}\:\mathrm{sin}\:{xdx}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {xln}\:\mathrm{sin}\:{xdx}+\frac{\pi}{\mathrm{4}}……\:\:\:\:\:…\left(\mathrm{1}\right)…{by}\:{parts} \\ $$$$\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {xln}\:\mathrm{sin}\:{xdx}+\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} {xln}\:\mathrm{sin}\:{xdx}=−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}….\:\left(\mathrm{2}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {xln}\:\mathrm{sin}\:{xdx}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{4}}−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}\right)=\frac{\pi}{\mathrm{8}}\left(\mathrm{1}−\mathrm{2}{ln}\mathrm{2}\right) \\ $$
