Question Number 128464 by n0y0n last updated on 07/Jan/21
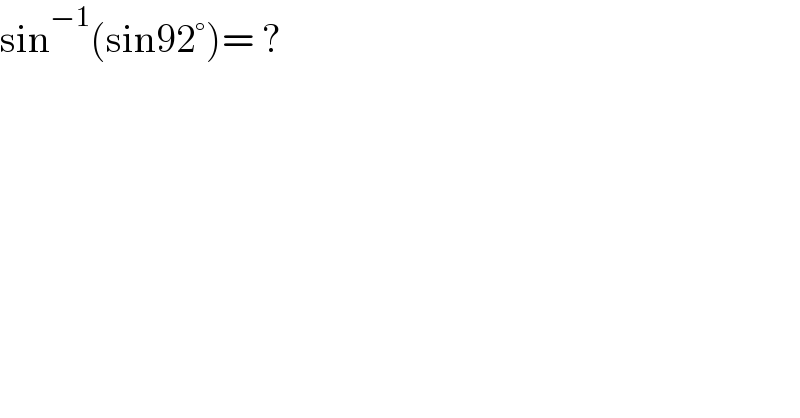
$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin92}°\right)=\:? \\ $$
Commented by mr W last updated on 07/Jan/21

$$\mathrm{88}° \\ $$
Answered by Olaf last updated on 08/Jan/21
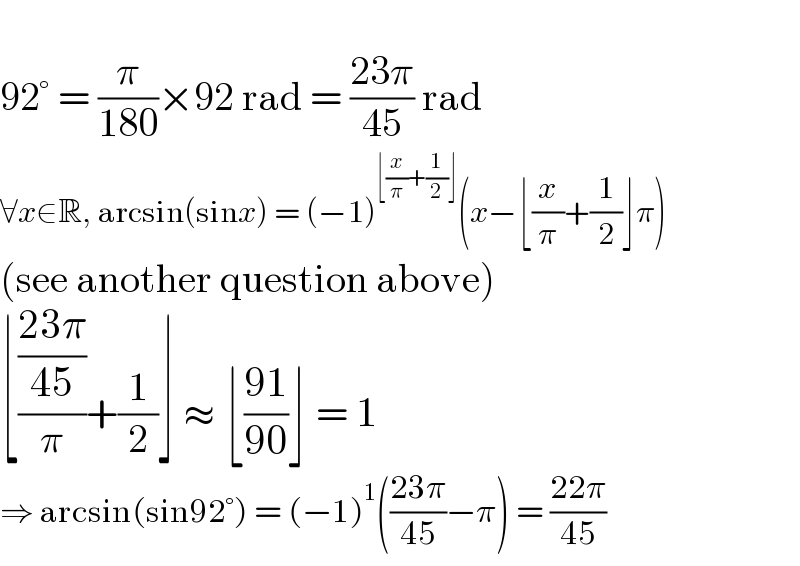
$$ \\ $$$$\mathrm{92}°\:=\:\frac{\pi}{\mathrm{180}}×\mathrm{92}\:\mathrm{rad}\:=\:\frac{\mathrm{23}\pi}{\mathrm{45}}\:\mathrm{rad} \\ $$$$\forall{x}\in\mathbb{R},\:\mathrm{arcsin}\left(\mathrm{sin}{x}\right)\:=\:\left(−\mathrm{1}\right)^{\lfloor\frac{{x}}{\pi}+\frac{\mathrm{1}}{\mathrm{2}}\rfloor} \left({x}−\lfloor\frac{{x}}{\pi}+\frac{\mathrm{1}}{\mathrm{2}}\rfloor\pi\right) \\ $$$$\left(\mathrm{see}\:\mathrm{another}\:\mathrm{question}\:\mathrm{above}\right) \\ $$$$\lfloor\frac{\frac{\mathrm{23}\pi}{\mathrm{45}}}{\pi}+\frac{\mathrm{1}}{\mathrm{2}}\rfloor\:\approx\:\lfloor\frac{\mathrm{91}}{\mathrm{90}}\rfloor\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{arcsin}\left(\mathrm{sin92}°\right)\:=\:\left(−\mathrm{1}\right)^{\mathrm{1}} \left(\frac{\mathrm{23}\pi}{\mathrm{45}}−\pi\right)\:=\:\frac{\mathrm{22}\pi}{\mathrm{45}} \\ $$
