Question Number 128498 by mathmax by abdo last updated on 07/Jan/21
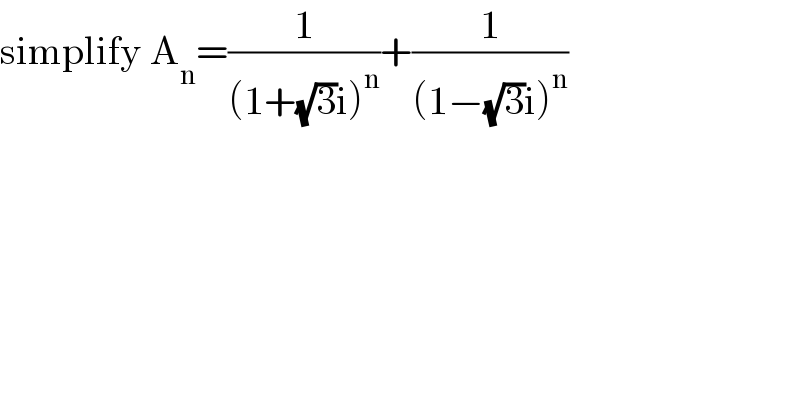
$$\mathrm{simplify}\:\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}\right)^{\mathrm{n}} }+\frac{\mathrm{1}}{\left(\mathrm{1}−\sqrt{\mathrm{3}}\mathrm{i}\right)^{\mathrm{n}} } \\ $$
Answered by TheSupreme last updated on 08/Jan/21
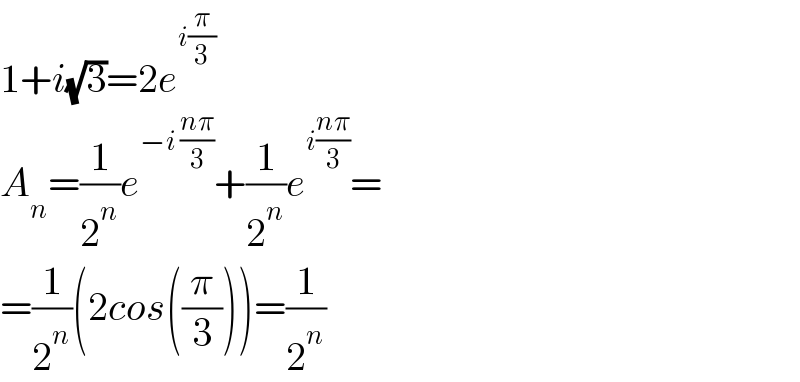
$$\mathrm{1}+{i}\sqrt{\mathrm{3}}=\mathrm{2}{e}^{{i}\frac{\pi}{\mathrm{3}}} \\ $$$${A}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}} }{e}^{−{i}\:\frac{{n}\pi}{\mathrm{3}}} +\frac{\mathrm{1}}{\mathrm{2}^{{n}} }{e}^{{i}\frac{{n}\pi}{\mathrm{3}}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\left(\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$
