Question Number 63079 by mathmax by abdo last updated on 28/Jun/19
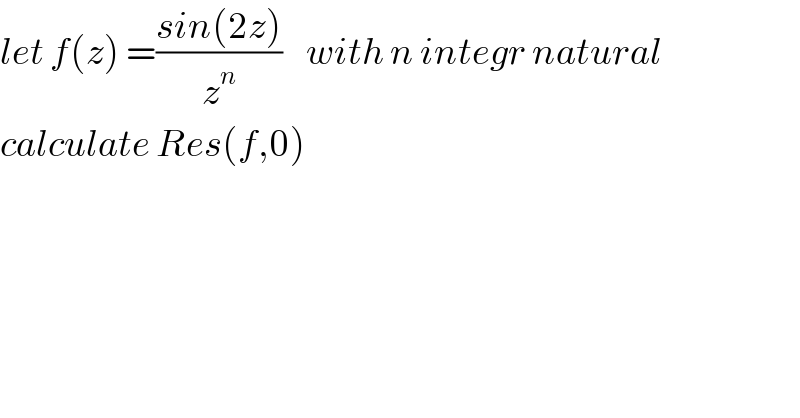
$${let}\:{f}\left({z}\right)\:=\frac{{sin}\left(\mathrm{2}{z}\right)}{{z}^{{n}} }\:\:\:\:{with}\:{n}\:{integr}\:{natural}\: \\ $$$${calculate}\:{Res}\left({f},\mathrm{0}\right) \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19
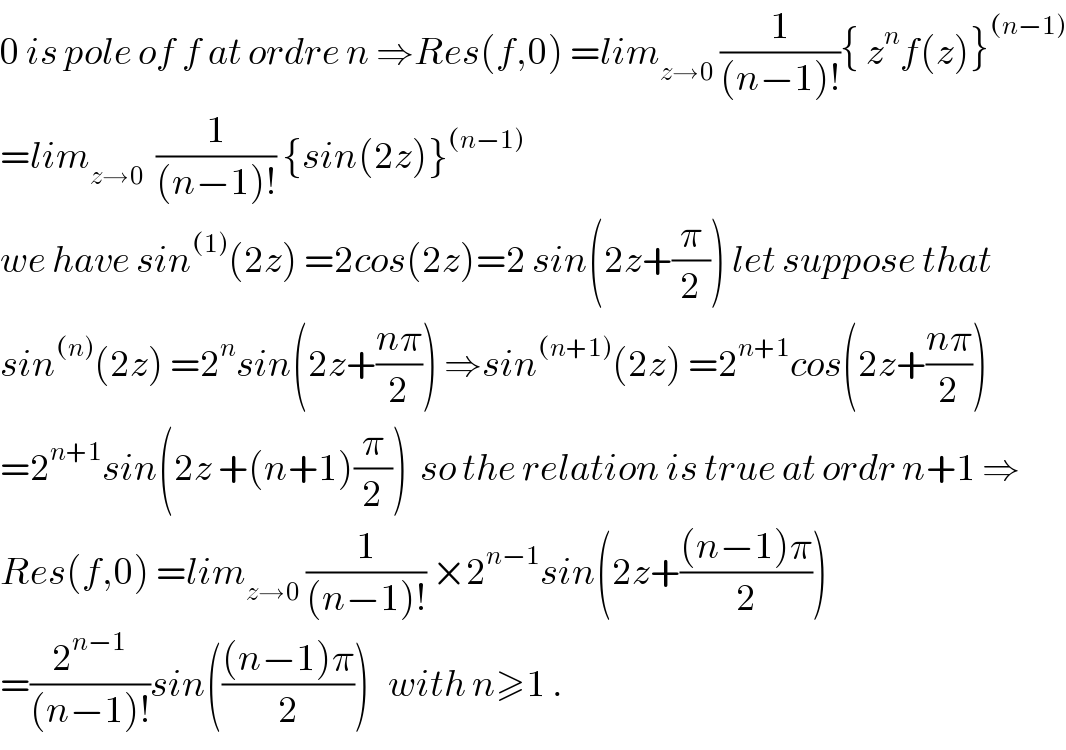
$$\mathrm{0}\:{is}\:{pole}\:{of}\:{f}\:{at}\:{ordre}\:{n}\:\Rightarrow{Res}\left({f},\mathrm{0}\right)\:={lim}_{{z}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\left\{\:{z}^{{n}} {f}\left({z}\right)\right\}^{\left({n}−\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow\mathrm{0}} \:\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\:\left\{{sin}\left(\mathrm{2}{z}\right)\right\}^{\left({n}−\mathrm{1}\right)} \\ $$$${we}\:{have}\:{sin}^{\left(\mathrm{1}\right)} \left(\mathrm{2}{z}\right)\:=\mathrm{2}{cos}\left(\mathrm{2}{z}\right)=\mathrm{2}\:{sin}\left(\mathrm{2}{z}+\frac{\pi}{\mathrm{2}}\right)\:{let}\:{suppose}\:{that} \\ $$$${sin}^{\left({n}\right)} \left(\mathrm{2}{z}\right)\:=\mathrm{2}^{{n}} {sin}\left(\mathrm{2}{z}+\frac{{n}\pi}{\mathrm{2}}\right)\:\Rightarrow{sin}^{\left({n}+\mathrm{1}\right)} \left(\mathrm{2}{z}\right)\:=\mathrm{2}^{{n}+\mathrm{1}} {cos}\left(\mathrm{2}{z}+\frac{{n}\pi}{\mathrm{2}}\right) \\ $$$$=\mathrm{2}^{{n}+\mathrm{1}} {sin}\left(\mathrm{2}{z}\:+\left({n}+\mathrm{1}\right)\frac{\pi}{\mathrm{2}}\right)\:\:{so}\:{the}\:{relation}\:{is}\:{true}\:{at}\:{ordr}\:{n}+\mathrm{1}\:\Rightarrow \\ $$$${Res}\left({f},\mathrm{0}\right)\:={lim}_{{z}\rightarrow\mathrm{0}} \:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)!}\:×\mathrm{2}^{{n}−\mathrm{1}} {sin}\left(\mathrm{2}{z}+\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{2}^{{n}−\mathrm{1}} }{\left({n}−\mathrm{1}\right)!}{sin}\left(\frac{\left({n}−\mathrm{1}\right)\pi}{\mathrm{2}}\right)\:\:\:{with}\:{n}\geqslant\mathrm{1}\:. \\ $$
