Question Number 128634 by liberty last updated on 09/Jan/21
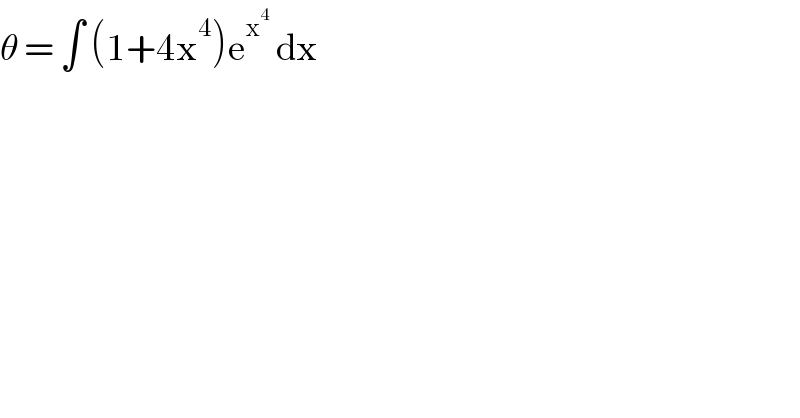
$$\theta\:=\:\int\:\left(\mathrm{1}+\mathrm{4x}^{\mathrm{4}} \right)\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\mathrm{dx}\: \\ $$
Answered by john_santu last updated on 09/Jan/21
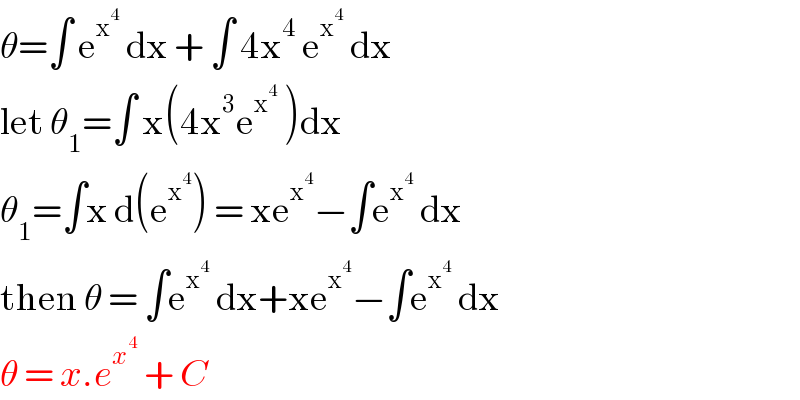
$$\theta=\int\:\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\mathrm{dx}\:+\:\int\:\mathrm{4x}^{\mathrm{4}} \:\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\mathrm{dx}\: \\ $$$$\mathrm{let}\:\theta_{\mathrm{1}} =\int\:\mathrm{x}\left(\mathrm{4x}^{\mathrm{3}} \mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\right)\mathrm{dx} \\ $$$$\theta_{\mathrm{1}} =\int\mathrm{x}\:\mathrm{d}\left(\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \right)\:=\:\mathrm{xe}^{\mathrm{x}^{\mathrm{4}} } −\int\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\mathrm{dx}\: \\ $$$$\mathrm{then}\:\theta\:=\:\int\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\mathrm{dx}+\mathrm{xe}^{\mathrm{x}^{\mathrm{4}} } −\int\mathrm{e}^{\mathrm{x}^{\mathrm{4}} } \:\mathrm{dx}\: \\ $$$$\theta\:=\:{x}.{e}^{{x}^{\mathrm{4}} } \:+\:{C}\: \\ $$
