Q-63108-A-check-eq-of-ellipse-x-2-4-y-2-1-Inscribed-equilateral-ABC-of-side-s-16-6-365-Do-these-points-satisfy-for-A-B-C-A-4-365-19-365-B-20-8-3-

Question Number 63218 by ajfour last updated on 30/Jun/19

$${Q}.\mathrm{63108}\:\:\:\left({A}\:{check}\right) \\ $$$${eq}.\:{of}\:{ellipse} \\ $$$$\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{y}^{\mathrm{2}} =\mathrm{1} \\ $$$${Inscribed}\:{equilateral}\:\bigtriangleup{ABC} \\ $$$${of}\:{side}\:\boldsymbol{{s}}=\frac{\mathrm{16}\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{365}}} \\ $$$${Do}\:{these}\:{points}\:{satisfy}\:{for} \\ $$$${A},\:{B},\:{C}\:? \\ $$$${A}\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{365}}},\:\frac{\mathrm{19}}{\:\sqrt{\mathrm{365}}}\right)\:\:\:;\:\: \\ $$$${B}\left[−\frac{\left(\mathrm{20}+\mathrm{8}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{365}}},\:\frac{\mathrm{8}\sqrt{\mathrm{3}}−\mathrm{5}}{\:\sqrt{\mathrm{365}}}\right] \\ $$$${C}\left[−\frac{\left(\mathrm{20}−\mathrm{8}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{365}}}\:,\:−\frac{\left(\mathrm{5}+\mathrm{8}\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{365}}}\right] \\ $$$$\:\theta=\mathrm{45}° \\ $$

Commented by Tinkutara@ last updated on 02/Jul/19

hello Mr W ! remember me? btw are you active on WhatsApp, Facebook, Snapchat, Twitter, LinkedIn, Pinterest ? p.s- recently, my Vacations got over. ������ ( went to phi phi Island!!! { Thailand})

Commented by ajfour last updated on 01/Jul/19

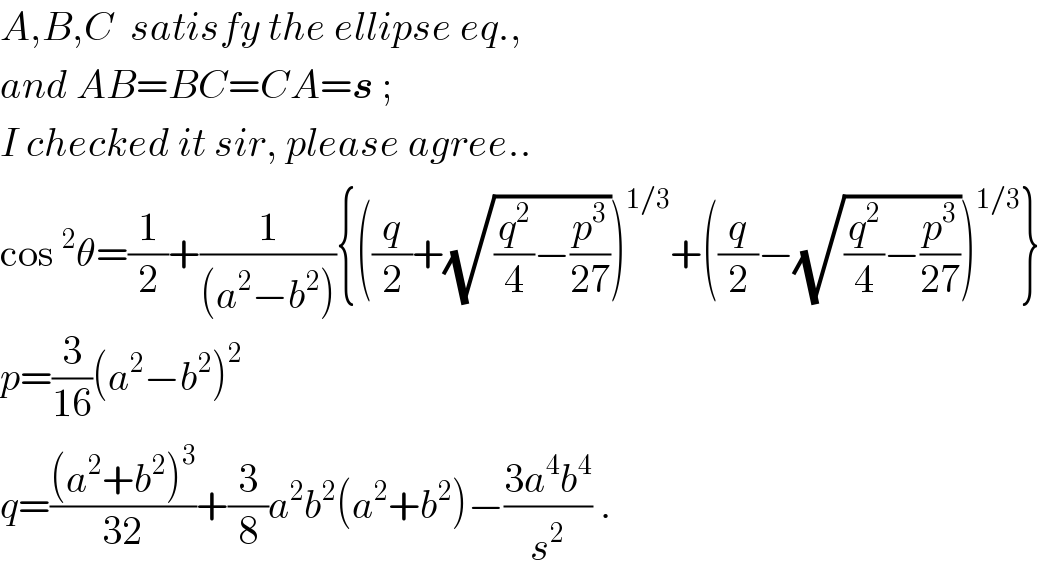
$${A},{B},{C}\:\:{satisfy}\:{the}\:{ellipse}\:{eq}., \\ $$$${and}\:{AB}={BC}={CA}=\boldsymbol{{s}}\:; \\ $$$${I}\:{checked}\:{it}\:{sir},\:{please}\:{agree}.. \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\left\{\left(\frac{{q}}{\mathrm{2}}+\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\right)^{\mathrm{1}/\mathrm{3}} +\left(\frac{{q}}{\mathrm{2}}−\sqrt{\frac{{q}^{\mathrm{2}} }{\mathrm{4}}−\frac{{p}^{\mathrm{3}} }{\mathrm{27}}}\right)^{\mathrm{1}/\mathrm{3}} \right\} \\ $$$${p}=\frac{\mathrm{3}}{\mathrm{16}}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${q}=\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{3}} }{\mathrm{32}}+\frac{\mathrm{3}}{\mathrm{8}}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\frac{\mathrm{3}{a}^{\mathrm{4}} {b}^{\mathrm{4}} }{{s}^{\mathrm{2}} }\:. \\ $$

Commented by kaivan.ahmadi last updated on 01/Jul/19

$${hi}\:{mr}\:{w}\:{where}\:{are}\:{you}\:{from}? \\ $$$${do}\:{you}\:{have}\:{instagram}\:{page}? \\ $$

Commented by mr W last updated on 01/Jul/19

$${yes}\:{sir}!\:{after}\:{new}\:{consideration}\:{now} \\ $$$${i}\:{think}\:{solutions}\:{other}\:{than} \\ $$$$\theta=\mathrm{0}°\:{are}\:{possible}.\:{i}'{ll}\:{try}\:{to}\:{find}\:{out} \\ $$$${the}\:{mistakes}\:{in}\:{my}\:{working}. \\ $$

Commented by Tinkutara@ last updated on 02/Jul/19

thanks sir! I wish the same for you...

Commented by ajfour last updated on 04/Jul/19

Tinkutara, how did you perform in jee advanced, where are you probably going to join.

Commented by Tinkutara@ last updated on 03/Jul/19

my paper went okayish. Unfortunately , I 'm not getting CSE in top 5 IITS ( due to reservation , sigh!). So Most probably I will be going to Bits Pilani CSE . ( since it's better than rest iits ) . - At the end of the day , I'm thankful to you and rest of the members of this awesome community to provide elegant solutions to the silly doubts thrown at you guys :P

Commented by Tinkutara last updated on 18/Jul/19

@ajfour Sir: I got a rank between 5900-6k in advanced and got IIT KGP. I am also thankful to all of them who solved my doubts on this platform which meant a lot to me! But @above is not my id.

Terms of Service
Privacy Policy
Contact: info@tinkutara.com