Menu Close

advanced-calculus-prove-that-n-0-1-n-4n-2-1-1-4-2-picsch-pi-2-

Tinku Tara 0 Comments
Pin




Question Number 137307 by mnjuly1970 last updated on 31/Mar/21
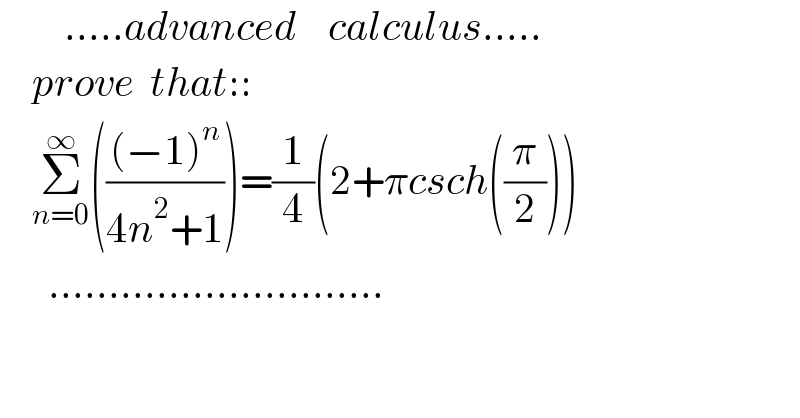
.....advanced calculus..... prove that:: Σ_(n=0) ^∞ ((((−1)^n )/(4n^2 +1)))=(1/4)(2+πcsch((π/2))) ............................
$$\:\:\:\:\:\:\:\:…..{advanced}\:\:\:\:{calculus}….. \\ $$$$\:\:\:\:{prove}\:\:{that}:: \\ $$$$\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}+\pi{csch}\left(\frac{\pi}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\:\:………………………. \\ $$
Answered by Dwaipayan Shikari last updated on 31/Mar/21
1−(1/5)+(1/(17))−(1/(37))+(1/(65))−(1/(101))+... 1,17,65 g_n =an^2 +bn+c⇒g_0 =c=1 g_1 =a+b+c=17⇒a+b=16 g_2 =4a+2b+1=65⇒2a+b=32⇒a=16 b=0 c=1 ⇒g_n =16n^2 +1 5,37,101 g_n =(4n+2)^2 +1 Σ_(n=0) ^∞ (1/(16n^2 +1))−(1/(16n^2 +16n+5)) =(1/(16))((π/(2.(1/4)))coth((π/4))−(1/(2.(1/(16)))))−(1/(4i(√5)))Σ_(n=0) ^∞ (1/((n−(((−4+i(√5))/8)))))−(1/((n−(((−4−i(√5))/8))))) =(π/8)coth((π/4))−(1/2)−(1/(4i(√5)))(ψ((1/2)+((i(√5))/4))−ψ((1/2)−((i(√5))/8))) =(π/8)coth((π/4))−(1/2)+(π/(4i(√5)))cot((1/2)+((i(√5))/8))π =(π/8)coth((π/4))−(1/2)−(π/( 4(√5)))tanh(((√5)/8)π) :(
$$\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{17}}−\frac{\mathrm{1}}{\mathrm{37}}+\frac{\mathrm{1}}{\mathrm{65}}−\frac{\mathrm{1}}{\mathrm{101}}+… \\ $$$$\mathrm{1},\mathrm{17},\mathrm{65} \\ $$$${g}_{{n}} ={an}^{\mathrm{2}} +{bn}+{c}\Rightarrow{g}_{\mathrm{0}} ={c}=\mathrm{1} \\ $$$${g}_{\mathrm{1}} ={a}+{b}+{c}=\mathrm{17}\Rightarrow{a}+{b}=\mathrm{16} \\ $$$${g}_{\mathrm{2}} =\mathrm{4}{a}+\mathrm{2}{b}+\mathrm{1}=\mathrm{65}\Rightarrow\mathrm{2}{a}+{b}=\mathrm{32}\Rightarrow{a}=\mathrm{16}\:\:\:{b}=\mathrm{0}\:{c}=\mathrm{1}\:\Rightarrow{g}_{{n}} =\mathrm{16}{n}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{5},\mathrm{37},\mathrm{101}\:\:\:\:{g}_{{n}} =\left(\mathrm{4}{n}+\mathrm{2}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{16}{n}^{\mathrm{2}} +\mathrm{16}{n}+\mathrm{5}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}\left(\frac{\pi}{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{4}}}{coth}\left(\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{16}}}\right)−\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{5}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}−\left(\frac{−\mathrm{4}+{i}\sqrt{\mathrm{5}}}{\mathrm{8}}\right)\right)}−\frac{\mathrm{1}}{\left({n}−\left(\frac{−\mathrm{4}−{i}\sqrt{\mathrm{5}}}{\mathrm{8}}\right)\right)} \\ $$$$=\frac{\pi}{\mathrm{8}}{coth}\left(\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}{i}\sqrt{\mathrm{5}}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{5}}}{\mathrm{4}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{i}\sqrt{\mathrm{5}}}{\mathrm{8}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{8}}{coth}\left(\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi}{\mathrm{4}{i}\sqrt{\mathrm{5}}}{cot}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{{i}\sqrt{\mathrm{5}}}{\mathrm{8}}\right)\pi \\ $$$$=\frac{\pi}{\mathrm{8}}{coth}\left(\frac{\pi}{\mathrm{4}}\right)−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\pi}{\:\mathrm{4}\sqrt{\mathrm{5}}}{tanh}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\pi\right) \\ $$$$:\left(\right. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *