Question Number 129086 by Ar Brandon last updated on 12/Jan/21
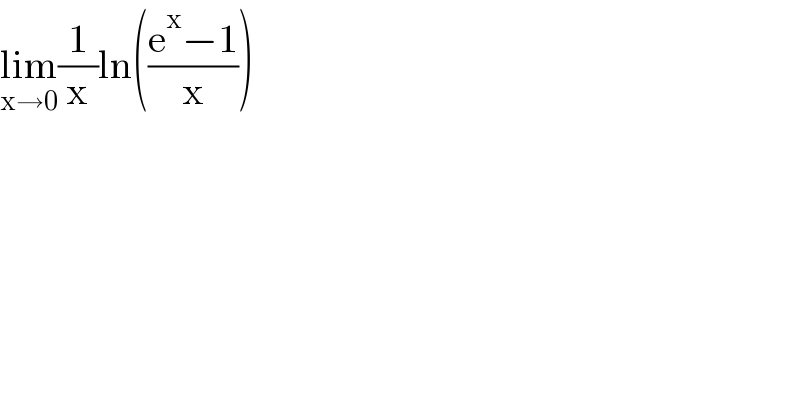
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}}\mathrm{ln}\left(\frac{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}}\right) \\ $$
Answered by Dwaipayan Shikari last updated on 12/Jan/21
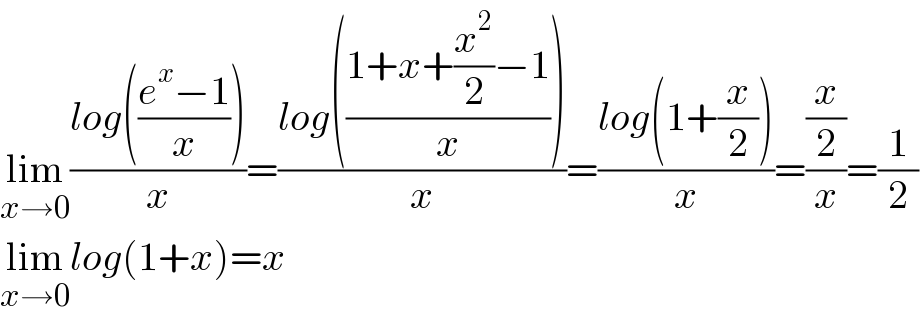
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{log}\left(\frac{{e}^{{x}} −\mathrm{1}}{{x}}\right)}{{x}}=\frac{{log}\left(\frac{\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}}{{x}}\right)}{{x}}=\frac{{log}\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)}{{x}}=\frac{\frac{{x}}{\mathrm{2}}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{log}\left(\mathrm{1}+{x}\right)={x} \\ $$
Commented by Ar Brandon last updated on 13/Jan/21
Cool bro ! ����
Answered by liberty last updated on 12/Jan/21
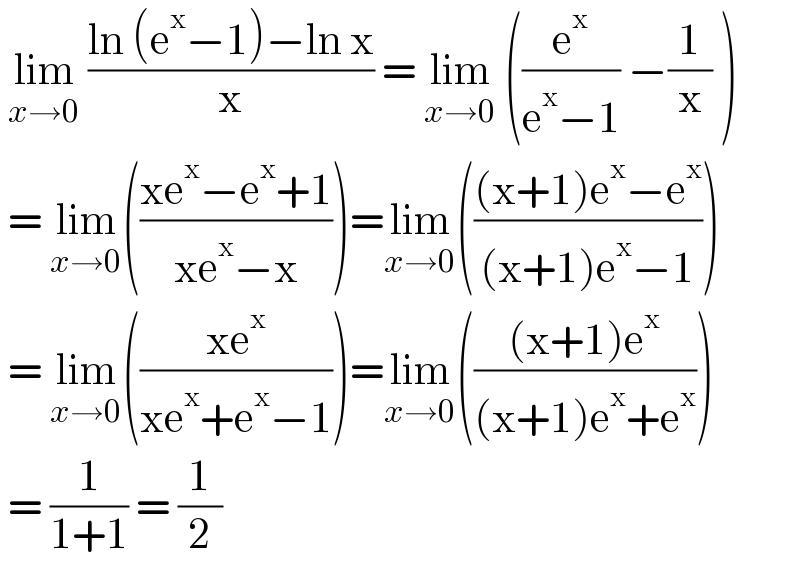
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)−\mathrm{ln}\:\mathrm{x}}{\mathrm{x}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{e}^{\mathrm{x}} }{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{x}}\:\right) \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{xe}^{\mathrm{x}} −\mathrm{e}^{\mathrm{x}} +\mathrm{1}}{\mathrm{xe}^{\mathrm{x}} −\mathrm{x}}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} −\mathrm{e}^{\mathrm{x}} }{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right) \\ $$$$\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{xe}^{\mathrm{x}} }{\mathrm{xe}^{\mathrm{x}} +\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} }{\left(\mathrm{x}+\mathrm{1}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{e}^{\mathrm{x}} }\right) \\ $$$$\:=\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 13/Jan/21
Same method I used. Thanks for affirmation.
