Question Number 63588 by ajfour last updated on 05/Jul/19
Commented by ajfour last updated on 05/Jul/19

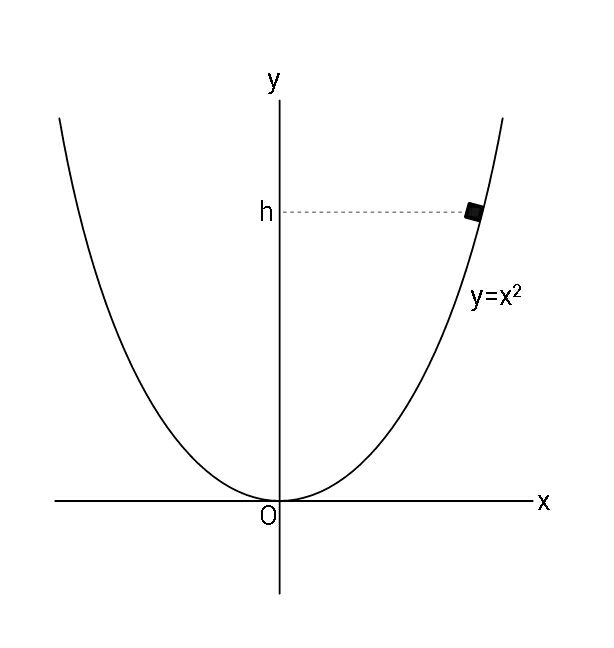
$${If}\:{released}\:{as}\:{shown},\:{find}\:{time} \\ $$$${taken}\:{by}\:{the}\:{small}\:{block}\:{to}\:{slide} \\ $$$${down}\:{the}\:{frictionless}\:{track}\:{till}\:{O}. \\ $$
Answered by mr W last updated on 06/Jul/19
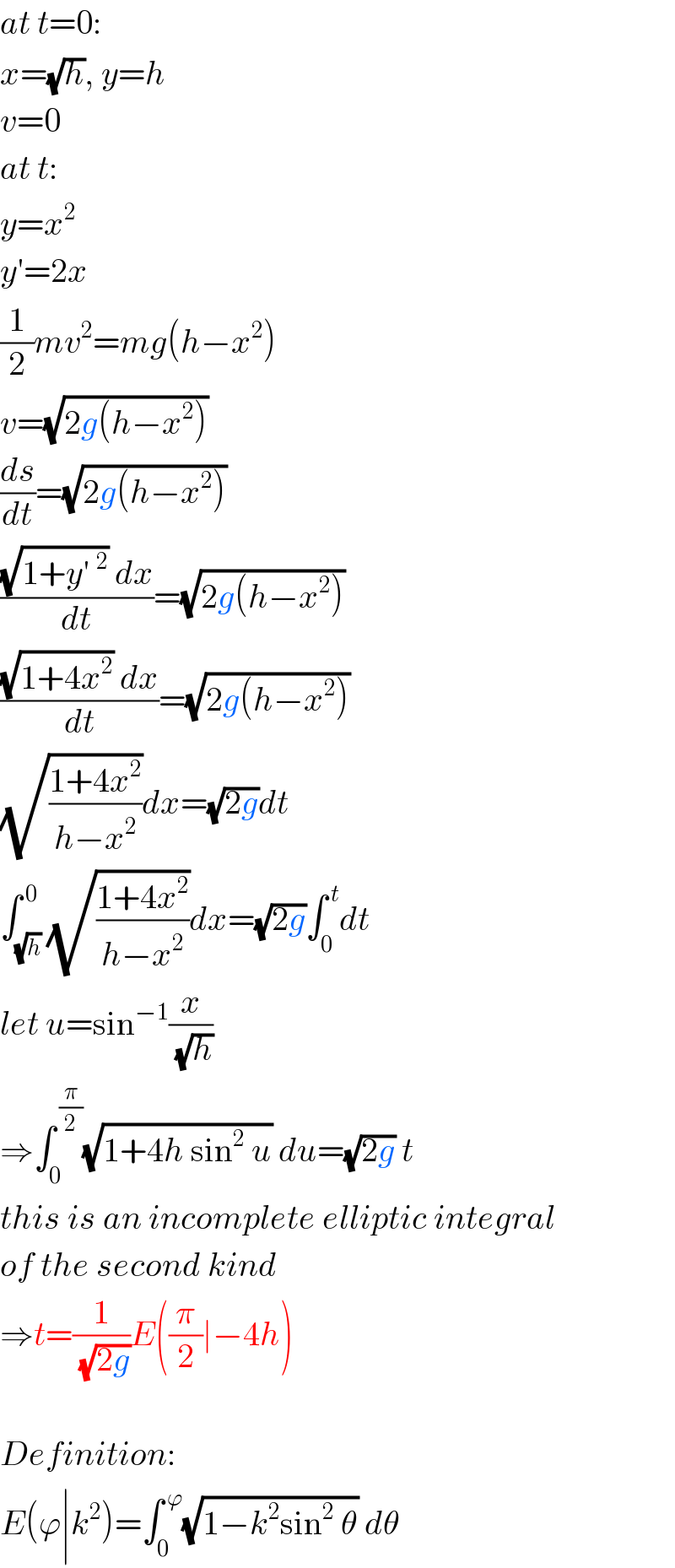
$${at}\:{t}=\mathrm{0}: \\ $$$${x}=\sqrt{{h}},\:{y}={h} \\ $$$${v}=\mathrm{0} \\ $$$${at}\:{t}: \\ $$$${y}={x}^{\mathrm{2}} \\ $$$${y}'=\mathrm{2}{x} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} ={mg}\left({h}−{x}^{\mathrm{2}} \right) \\ $$$${v}=\sqrt{\mathrm{2}{g}\left({h}−{x}^{\mathrm{2}} \right)} \\ $$$$\frac{{ds}}{{dt}}=\sqrt{\mathrm{2}{g}\left({h}−{x}^{\mathrm{2}} \right)} \\ $$$$\frac{\sqrt{\mathrm{1}+{y}'\:^{\mathrm{2}} }\:{dx}}{{dt}}=\sqrt{\mathrm{2}{g}\left({h}−{x}^{\mathrm{2}} \right)} \\ $$$$\frac{\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\:{dx}}{{dt}}=\sqrt{\mathrm{2}{g}\left({h}−{x}^{\mathrm{2}} \right)} \\ $$$$\sqrt{\frac{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{{h}−{x}^{\mathrm{2}} }}{dx}=\sqrt{\mathrm{2}{g}}{dt} \\ $$$$\int_{\sqrt{{h}}} ^{\:\mathrm{0}} \sqrt{\frac{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{{h}−{x}^{\mathrm{2}} }}{dx}=\sqrt{\mathrm{2}{g}}\int_{\mathrm{0}} ^{\:{t}} {dt} \\ $$$${let}\:{u}=\mathrm{sin}^{−\mathrm{1}} \frac{{x}}{\:\sqrt{{h}}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \sqrt{\mathrm{1}+\mathrm{4}{h}\:\mathrm{sin}^{\mathrm{2}} \:{u}}\:{du}=\sqrt{\mathrm{2}{g}}\:{t} \\ $$$${this}\:{is}\:{an}\:{incomplete}\:{elliptic}\:{integral} \\ $$$${of}\:{the}\:{second}\:{kind} \\ $$$$\Rightarrow{t}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}{g}}}{E}\left(\frac{\pi}{\mathrm{2}}\mid−\mathrm{4}{h}\right) \\ $$$$ \\ $$$${Definition}: \\ $$$${E}\left(\varphi\mid{k}^{\mathrm{2}} \right)=\int_{\mathrm{0}} ^{\:\varphi} \sqrt{\mathrm{1}−{k}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta}\:{d}\theta \\ $$
Commented by JDamian last updated on 06/Jul/19
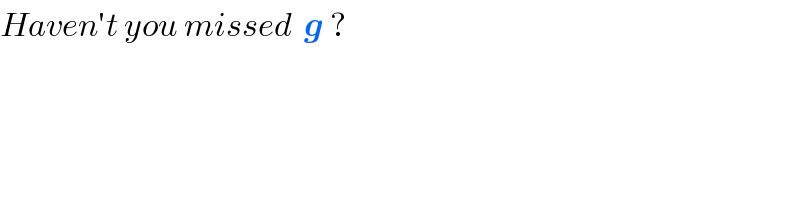
$${Haven}'{t}\:{you}\:{missed}\:\:\boldsymbol{{g}}\:? \\ $$
Commented by ajfour last updated on 06/Jul/19
thank you sir, i had a notion,
it would turn awry!
