Menu Close

Question-63641

Tinku Tara 0 Comments
Pin




Question Number 63641 by aliesam last updated on 06/Jul/19
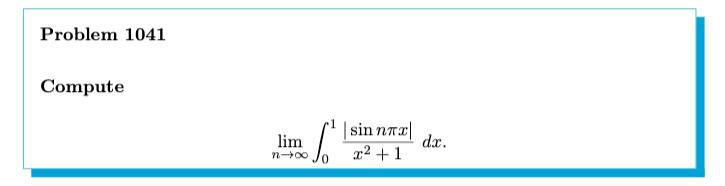
Commented by mathmax by abdo last updated on 06/Jul/19
let A_n = ∫_0 ^1 ((∣sin(nπx)∣)/(x^2 +1)) dx ⇒ lim_(n→+∞) A_n =lim_(n→+∞) Σ_(k=0) ^(n−1) ∫_(k/n) ^((k+1)/n) ((∣sin(nπx)∣)/(1+x^2 ))dx changement nx =t give ∫_(k/n) ^((k+1)/n) ((∣sin(nπx)∣)/(1+x^2 )) dx =∫_k ^(k+1) ((∣sin(πt)∣)/(1+(t^2 /n^2 ))) (dt/n) =n ∫_k ^(k+1) ((∣sin(πt)∣)/(n^2 +t^2 )) dt ⇒ lim_(n→+∞) A_n =lim_(n→+∞) n ∫_0 ^n ((∣sin(πt)∣)/(n^2 +t^2 )) dt =lim_(n→+∞) ∫_R ((n∣sin(πt)∣)/(n^2 +t^2 )) χ_([0,n[) (t)dt let f_n (t) =((n∣sin(πt)∣)/(n^2 +t^2 )) χ_([0,n[) (t) we have for t inside [0,n[ f_n (t) =((n ∣sin(πt)∣)/(n^2 (1+(t^2 /n^2 )))) =(1/n) ×n^2 ((∣sin(πt)∣)/(1+(t^2 /n^2 ))) ∼n(1−(t^2 /n^2 )+o((1/n^2 )))∣sin(πt)∣ ⇒ n ∫_0 ^n ((∣sin(πt)∣)/(n^2 +t^2 ))dt ∼∫_0 ^n n ∣sin(πt)∣dt−(1/n) ∫_0 ^n t^2 ∣sin(πt)∣dt +o((1/n))...be continued...
$${let}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mid{sin}\left({n}\pi{x}\right)\mid}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:\Rightarrow\:{lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} ={lim}_{{n}\rightarrow+\infty} \sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\int_{\frac{{k}}{{n}}} ^{\frac{{k}+\mathrm{1}}{{n}}} \:\:\:\frac{\mid{sin}\left({n}\pi{x}\right)\mid}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${changement}\:{nx}\:={t}\:{give}\: \\ $$$$\int_{\frac{{k}}{{n}}} ^{\frac{{k}+\mathrm{1}}{{n}}} \:\:\frac{\mid{sin}\left({n}\pi{x}\right)\mid}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:=\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{\mid{sin}\left(\pi{t}\right)\mid}{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\frac{{dt}}{{n}}\:={n}\:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{\mid{sin}\left(\pi{t}\right)\mid}{{n}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\:{dt}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{A}_{{n}} ={lim}_{{n}\rightarrow+\infty} \:{n}\:\int_{\mathrm{0}} ^{{n}} \:\:\frac{\mid{sin}\left(\pi{t}\right)\mid}{{n}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\:{dt}\:={lim}_{{n}\rightarrow+\infty} \:\:\:\int_{{R}} \:\frac{{n}\mid{sin}\left(\pi{t}\right)\mid}{{n}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\:\chi_{\left[\mathrm{0},{n}\left[\right.\right.} \left({t}\right){dt} \\ $$$${let}\:{f}_{{n}} \left({t}\right)\:=\frac{{n}\mid{sin}\left(\pi{t}\right)\mid}{{n}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }\:\chi_{\left[\mathrm{0},{n}\left[\right.\right.} \left({t}\right)\:\:{we}\:{have}\:\:{for}\:{t}\:{inside}\:\left[\mathrm{0},{n}\left[\right.\right. \\ $$$${f}_{{n}} \left({t}\right)\:=\frac{{n}\:\mid{sin}\left(\pi{t}\right)\mid}{{n}^{\mathrm{2}} \left(\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{{n}}\:×{n}^{\mathrm{2}} \:\frac{\mid{sin}\left(\pi{t}\right)\mid}{\mathrm{1}+\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\sim{n}\left(\mathrm{1}−\frac{{t}^{\mathrm{2}} }{{n}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\right)\mid{sin}\left(\pi{t}\right)\mid\:\Rightarrow \\ $$$${n}\:\int_{\mathrm{0}} ^{{n}} \:\:\frac{\mid{sin}\left(\pi{t}\right)\mid}{{n}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }{dt}\:\sim\int_{\mathrm{0}} ^{{n}} \:{n}\:\mid{sin}\left(\pi{t}\right)\mid{dt}−\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{{n}} \:{t}^{\mathrm{2}} \:\mid{sin}\left(\pi{t}\right)\mid{dt}\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)…{be}\:{continued}… \\ $$
Commented by mathmax by abdo last updated on 06/Jul/19
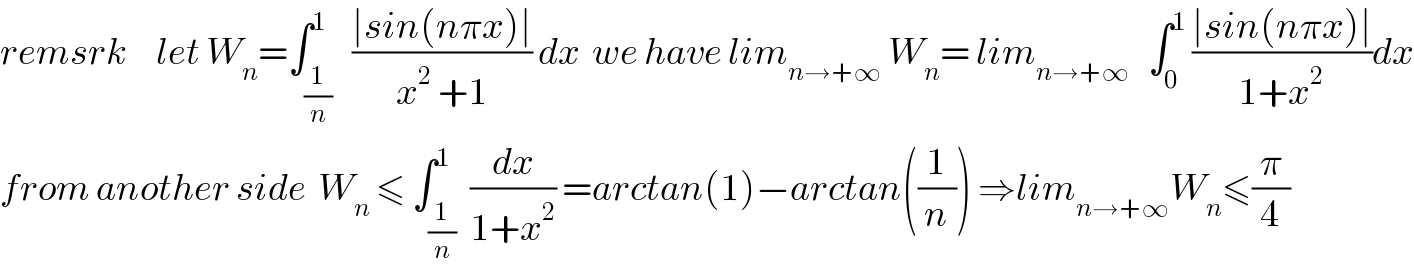
remsrk let W_n =∫_(1/n) ^1 ((∣sin(nπx)∣)/(x^2 +1)) dx we have lim_(n→+∞) W_n = lim_(n→+∞) ∫_0 ^1 ((∣sin(nπx)∣)/(1+x^2 ))dx from another side W_n ≤ ∫_(1/n) ^1 (dx/(1+x^2 )) =arctan(1)−arctan((1/n)) ⇒lim_(n→+∞) W_n ≤(π/4)
$${remsrk}\:\:\:\:\:{let}\:{W}_{{n}} =\int_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}} \:\:\frac{\mid{sin}\left({n}\pi{x}\right)\mid}{{x}^{\mathrm{2}} \:+\mathrm{1}}\:{dx}\:\:{we}\:{have}\:{lim}_{{n}\rightarrow+\infty} \:{W}_{{n}} =\:{lim}_{{n}\rightarrow+\infty} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mid{sin}\left({n}\pi{x}\right)\mid}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${from}\:{another}\:{side}\:\:{W}_{{n}} \:\leqslant\:\int_{\frac{\mathrm{1}}{{n}}} ^{\mathrm{1}} \:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:={arctan}\left(\mathrm{1}\right)−{arctan}\left(\frac{\mathrm{1}}{{n}}\right)\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {W}_{{n}} \leqslant\frac{\pi}{\mathrm{4}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *