Question Number 129272 by mnjuly1970 last updated on 14/Jan/21
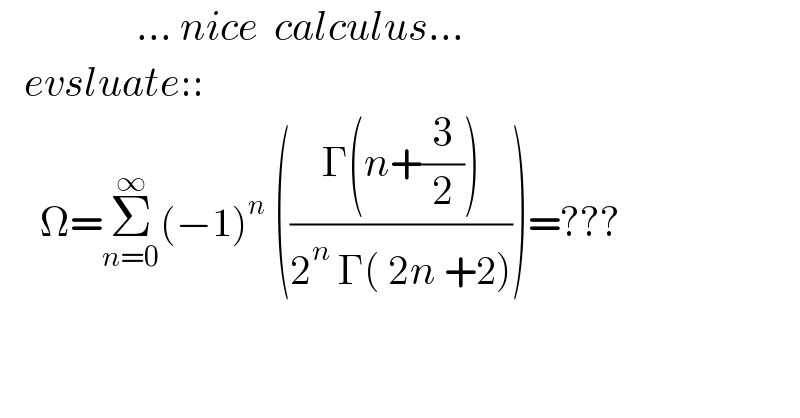
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{nice}\:\:{calculus}… \\ $$$$\:\:\:{evsluate}:: \\ $$$$\:\:\:\:\:\Omega=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \:\left(\frac{\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}^{{n}} \:\Gamma\left(\:\mathrm{2}{n}\:+\mathrm{2}\right)}\right)=??? \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 14/Jan/21
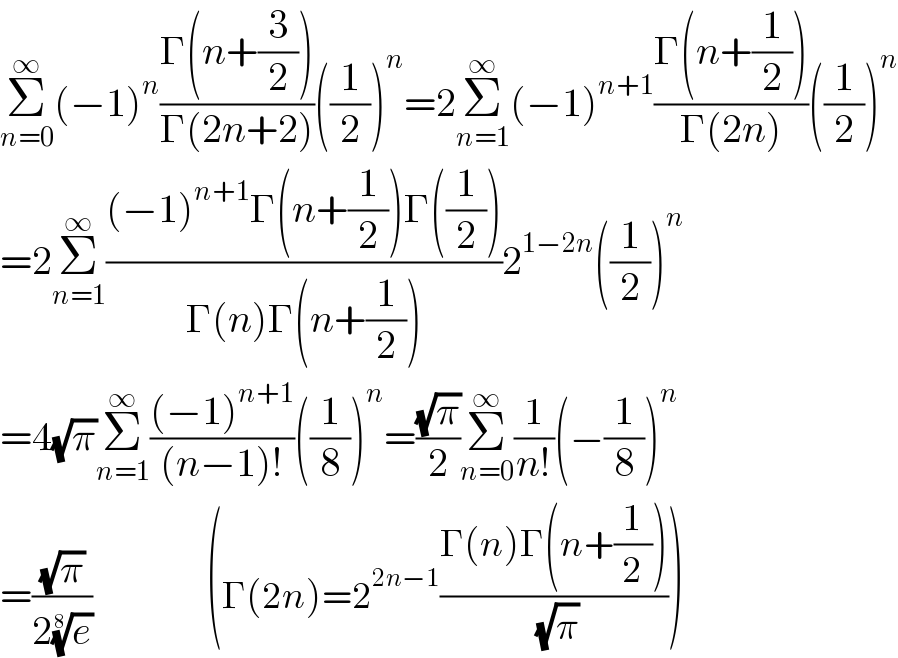
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\Gamma\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}{n}+\mathrm{2}\right)}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} =\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}{n}\right)}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left({n}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\mathrm{2}^{\mathrm{1}−\mathrm{2}{n}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$$=\mathrm{4}\sqrt{\pi}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\left({n}−\mathrm{1}\right)!}\left(\frac{\mathrm{1}}{\mathrm{8}}\right)^{{n}} =\frac{\sqrt{\pi}}{\mathrm{2}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\left(−\frac{\mathrm{1}}{\mathrm{8}}\right)^{{n}} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt[{\mathrm{8}}]{{e}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\Gamma\left(\mathrm{2}{n}\right)=\mathrm{2}^{\mathrm{2}{n}−\mathrm{1}} \frac{\Gamma\left({n}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\pi}}\right) \\ $$
Commented by mnjuly1970 last updated on 14/Jan/21

$$\:\:\:\:\:\:\:\:\:{very}\:{nice}\:\:\:{mr}\:{payan} \\ $$$$\:\:\:\:\:\:{legendre}\:{duplication}\:{formula}… \\ $$
