Question Number 63803 by aliesam last updated on 09/Jul/19

Commented by Prithwish sen last updated on 09/Jul/19

$$\left(\mathrm{x}+\mathrm{iy}\right)^{\mathrm{3}} \:=\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{7}}\mathrm{i}\right)^{\mathrm{2}} }{\mathrm{1}−\sqrt{\mathrm{7}}\mathrm{i}}\:=\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{7}}\mathrm{i}\right)^{\mathrm{3}} }{\mathrm{8}} \\ $$$$\:\therefore\:\mathrm{x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{y}\:=\:\frac{\sqrt{\mathrm{7}}}{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 09/Jul/19
![let Z =x+iy we get Z^3 =((−6+2(√7)i)/(1−(√7)i)) let solve this (e) ∣−6+2(√7)i∣ =(√(36+28))=(√(64))=8 ∣1−(√7)i∣ =(√(1+7))=(√8) ⇒∣((−6+2(√(i7)))/(1−(√7)i))∣ =(8/( (√8))) =2(√2) −6+2(√7)i =8(((−6)/8) +((2(√7)i)/8)) =8(−(3/4) +((√7)/4)i) =8 e^(iarctan(−((√7)/3))) 1−(√7)i =2(√2)( (1/(2(√2))) −((√7)/(2(√2)))i) =2(√2) e^(iarctan(−(√7))) ⇒ ((−6+2(√7)i)/(1−(√7)i)) =2(√2)e^(i( arctan(((−(√7))/3))+arctan((√7)))) =2(√2) e^(i(arctan((√7))−arctan(((√7)/3)))) let Z =ρ e^(iθ) (e) ⇒ρ^3 e^(i3θ) =2(√2)e^(i(arctan(√7)−arctan(((√7)/3))) ) ⇒ ρ =(2(√2))^(1/3) and 3θ =arctan((√7))−arctan(((√7)/3)) +2kπ ⇒ ⇒θ_k =((arctan((√7))−arctan(((√7)/3)))/3) +((2kπ)/3) and k ∈[[0,2]] the roots are Z_k =e^(iθ_k ) =x_k +iy_k Z_0 =e^(iθ_0 ) =x_0 +iy_0 Z_1 =e^(iθ_1 ) =x_1 +iy_1 Z_2 =e^(iθ_2 ) =x_2 +iy_2 ...](https://www.tinkutara.com/question/Q63805.png)
$${let}\:{Z}\:={x}+{iy}\:\:{we}\:{get}\:{Z}^{\mathrm{3}} =\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}}\:{let}\:{solve}\:{this}\:\left({e}\right) \\ $$$$\mid−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}\mid\:=\sqrt{\mathrm{36}+\mathrm{28}}=\sqrt{\mathrm{64}}=\mathrm{8} \\ $$$$\mid\mathrm{1}−\sqrt{\mathrm{7}}{i}\mid\:=\sqrt{\mathrm{1}+\mathrm{7}}=\sqrt{\mathrm{8}}\:\Rightarrow\mid\frac{−\mathrm{6}+\mathrm{2}\sqrt{{i}\mathrm{7}}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}}\mid\:=\frac{\mathrm{8}}{\:\sqrt{\mathrm{8}}}\:=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}\:=\mathrm{8}\left(\frac{−\mathrm{6}}{\mathrm{8}}\:+\frac{\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{8}}\right)\:=\mathrm{8}\left(−\frac{\mathrm{3}}{\mathrm{4}}\:+\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}{i}\right)\:=\mathrm{8}\:{e}^{{iarctan}\left(−\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)} \\ $$$$\mathrm{1}−\sqrt{\mathrm{7}}{i}\:=\mathrm{2}\sqrt{\mathrm{2}}\left(\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:−\frac{\sqrt{\mathrm{7}}}{\mathrm{2}\sqrt{\mathrm{2}}}{i}\right)\:=\mathrm{2}\sqrt{\mathrm{2}}\:{e}^{{iarctan}\left(−\sqrt{\mathrm{7}}\right)} \:\Rightarrow \\ $$$$\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}{i}}{\mathrm{1}−\sqrt{\mathrm{7}}{i}}\:=\mathrm{2}\sqrt{\mathrm{2}}{e}^{{i}\left(\:{arctan}\left(\frac{−\sqrt{\mathrm{7}}}{\mathrm{3}}\right)+{arctan}\left(\sqrt{\mathrm{7}}\right)\right)} =\mathrm{2}\sqrt{\mathrm{2}}\:{e}^{{i}\left({arctan}\left(\sqrt{\mathrm{7}}\right)−{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)\right)} \\ $$$${let}\:{Z}\:=\rho\:{e}^{{i}\theta} \:\:\:\left({e}\right)\:\Rightarrow\rho^{\mathrm{3}} \:{e}^{{i}\mathrm{3}\theta} \:=\mathrm{2}\sqrt{\mathrm{2}}{e}^{{i}\left({arctan}\sqrt{\mathrm{7}}−{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)\right)\:} \:\Rightarrow \\ $$$$\rho\:=\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\:{and}\:\:\mathrm{3}\theta\:={arctan}\left(\sqrt{\mathrm{7}}\right)−{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)\:+\mathrm{2}{k}\pi\:\Rightarrow \\ $$$$\Rightarrow\theta_{{k}} =\frac{{arctan}\left(\sqrt{\mathrm{7}}\right)−{arctan}\left(\frac{\sqrt{\mathrm{7}}}{\mathrm{3}}\right)}{\mathrm{3}}\:+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\:\:\:{and}\:{k}\:\in\left[\left[\mathrm{0},\mathrm{2}\right]\right] \\ $$$${the}\:{roots}\:{are}\:{Z}_{{k}} ={e}^{{i}\theta_{{k}} } \:={x}_{{k}} +{iy}_{{k}} \\ $$$${Z}_{\mathrm{0}} ={e}^{{i}\theta_{\mathrm{0}} } ={x}_{\mathrm{0}} +{iy}_{\mathrm{0}} \\ $$$${Z}_{\mathrm{1}} ={e}^{{i}\theta_{\mathrm{1}} } \:={x}_{\mathrm{1}} +{iy}_{\mathrm{1}} \\ $$$${Z}_{\mathrm{2}} ={e}^{{i}\theta_{\mathrm{2}} } \:={x}_{\mathrm{2}} +{iy}_{\mathrm{2}} … \\ $$
Commented by mathmax by abdo last updated on 09/Jul/19

$${sorry}\:{Z}_{{k}} =\rho\:{e}^{{i}\theta_{{k}} } \:\Rightarrow \\ $$$${Z}_{\mathrm{0}} =\rho{e}^{{i}\theta_{\mathrm{0}} } \:={x}_{\mathrm{0}} +{iy}_{\mathrm{0}} \\ $$$${Z}_{\mathrm{1}} =\rho\:{e}^{{i}\theta_{\mathrm{1}} } \:={x}_{\mathrm{1}} \:+{iy}_{\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 09/Jul/19

$${Z}_{\mathrm{2}} =\rho\:{e}^{{i}\theta_{\mathrm{2}} } \:={x}_{\mathrm{2}} +{iy}_{\mathrm{2}} \\ $$$${the}\:{reels}\:\left({x}_{{i}} \right){and}\:\left({y}_{{i}} \right){are}\:{detremined}. \\ $$
Answered by MJS last updated on 09/Jul/19
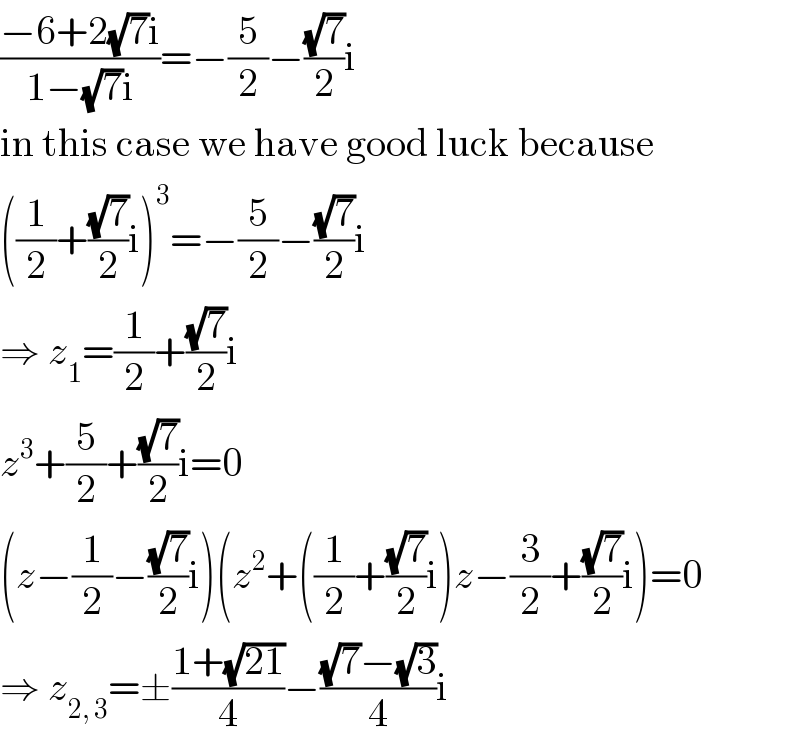
$$\frac{−\mathrm{6}+\mathrm{2}\sqrt{\mathrm{7}}\mathrm{i}}{\mathrm{1}−\sqrt{\mathrm{7}}\mathrm{i}}=−\frac{\mathrm{5}}{\mathrm{2}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{have}\:\mathrm{good}\:\mathrm{luck}\:\mathrm{because} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i}\right)^{\mathrm{3}} =−\frac{\mathrm{5}}{\mathrm{2}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i} \\ $$$$\Rightarrow\:{z}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i} \\ $$$${z}^{\mathrm{3}} +\frac{\mathrm{5}}{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i}=\mathrm{0} \\ $$$$\left({z}−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i}\right)\left({z}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i}\right){z}−\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{7}}}{\mathrm{2}}\mathrm{i}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{z}_{\mathrm{2},\:\mathrm{3}} =\pm\frac{\mathrm{1}+\sqrt{\mathrm{21}}}{\mathrm{4}}−\frac{\sqrt{\mathrm{7}}−\sqrt{\mathrm{3}}}{\mathrm{4}}\mathrm{i} \\ $$
