Menu Close

Let-a-sequence-a-n-satisfies-a-1-1-na-n-n-2-k-1-n-1-a-k-n-gt-2-Find-the-value-of-a-2021-

Tinku Tara 0 Comments
Pin




Question Number 129413 by ZiYangLee last updated on 15/Jan/21
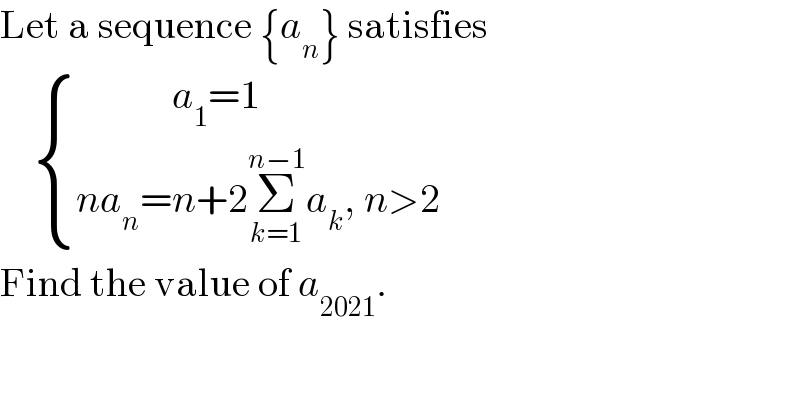
Let a sequence {a_n } satisfies { (( a_1 =1)),((na_n =n+2Σ_(k=1) ^(n−1) a_k , n>2)) :} Find the value of a_(2021) .
$$\mathrm{Let}\:\mathrm{a}\:\mathrm{sequence}\:\left\{{a}_{{n}} \right\}\:\mathrm{satisfies} \\ $$$$\:\:\:\:\begin{cases}{\:\:\:\:\:\:\:\:\:\:\:\:{a}_{\mathrm{1}} =\mathrm{1}}\\{{na}_{{n}} ={n}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{k}} ,\:{n}>\mathrm{2}}\end{cases} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:{a}_{\mathrm{2021}} . \\ $$
Commented by JDamian last updated on 15/Jan/21
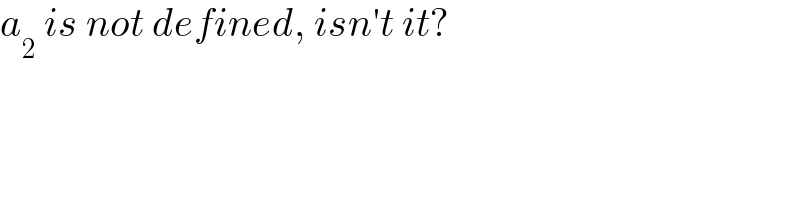
a_2 is not defined, isn′t it?
$${a}_{\mathrm{2}} \:{is}\:{not}\:{defined},\:{isn}'{t}\:{it}? \\ $$
Answered by Olaf last updated on 15/Jan/21
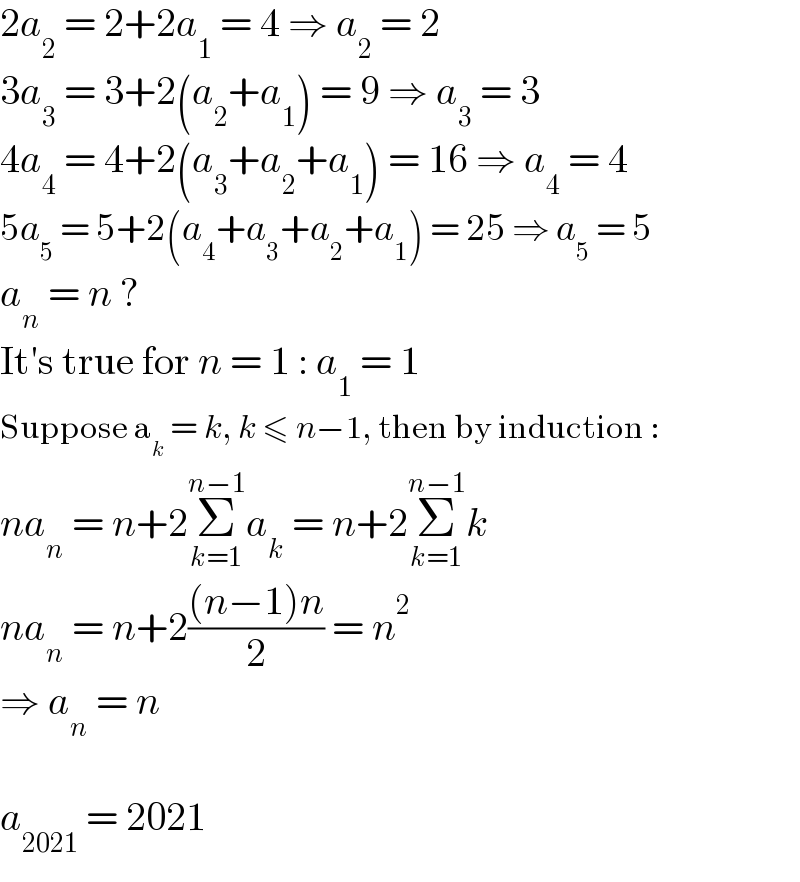
2a_2 = 2+2a_1 = 4 ⇒ a_2 = 2 3a_3 = 3+2(a_2 +a_1 ) = 9 ⇒ a_3 = 3 4a_4 = 4+2(a_3 +a_2 +a_1 ) = 16 ⇒ a_4 = 4 5a_5 = 5+2(a_4 +a_3 +a_2 +a_1 ) = 25 ⇒ a_5 = 5 a_n = n ? It′s true for n = 1 : a_1 = 1 Suppose a_k = k, k ≤ n−1, then by induction : na_n = n+2Σ_(k=1) ^(n−1) a_k = n+2Σ_(k=1) ^(n−1) k na_n = n+2(((n−1)n)/2) = n^2 ⇒ a_n = n a_(2021) = 2021
$$\mathrm{2}{a}_{\mathrm{2}} \:=\:\mathrm{2}+\mathrm{2}{a}_{\mathrm{1}} \:=\:\mathrm{4}\:\Rightarrow\:{a}_{\mathrm{2}} \:=\:\mathrm{2} \\ $$$$\mathrm{3}{a}_{\mathrm{3}} \:=\:\mathrm{3}+\mathrm{2}\left({a}_{\mathrm{2}} +{a}_{\mathrm{1}} \right)\:=\:\mathrm{9}\:\Rightarrow\:{a}_{\mathrm{3}} \:=\:\mathrm{3} \\ $$$$\mathrm{4}{a}_{\mathrm{4}} \:=\:\mathrm{4}+\mathrm{2}\left({a}_{\mathrm{3}} +{a}_{\mathrm{2}} +{a}_{\mathrm{1}} \right)\:=\:\mathrm{16}\:\Rightarrow\:{a}_{\mathrm{4}} \:=\:\mathrm{4} \\ $$$$\mathrm{5}{a}_{\mathrm{5}} \:=\:\mathrm{5}+\mathrm{2}\left({a}_{\mathrm{4}} +{a}_{\mathrm{3}} +{a}_{\mathrm{2}} +{a}_{\mathrm{1}} \right)\:=\:\mathrm{25}\:\Rightarrow\:{a}_{\mathrm{5}} \:=\:\mathrm{5} \\ $$$${a}_{{n}} \:=\:{n}\:? \\ $$$$\mathrm{It}'\mathrm{s}\:\mathrm{true}\:\mathrm{for}\:{n}\:=\:\mathrm{1}\::\:{a}_{\mathrm{1}} \:=\:\mathrm{1} \\ $$$$\mathrm{Suppose}\:\mathrm{a}_{{k}} \:=\:{k},\:{k}\:\leqslant\:{n}−\mathrm{1},\:\mathrm{then}\:\mathrm{by}\:\mathrm{induction}\:: \\ $$$${na}_{{n}} \:=\:{n}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{k}} \:=\:{n}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{k} \\ $$$${na}_{{n}} \:=\:{n}+\mathrm{2}\frac{\left({n}−\mathrm{1}\right){n}}{\mathrm{2}}\:=\:{n}^{\mathrm{2}} \\ $$$$\Rightarrow\:{a}_{{n}} \:=\:{n} \\ $$$$ \\ $$$${a}_{\mathrm{2021}} \:=\:\mathrm{2021} \\ $$
Commented by JDamian last updated on 16/Jan/21
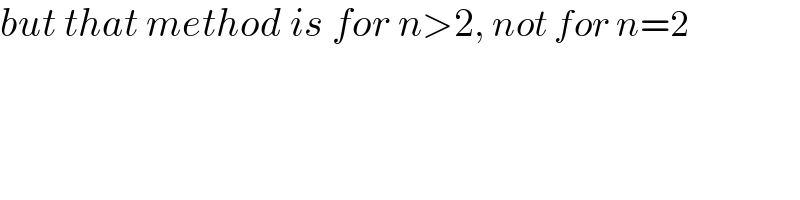
but that method is for n>2, not for n=2
$${but}\:{that}\:{method}\:{is}\:{for}\:{n}>\mathrm{2},\:{not}\:{for}\:{n}=\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *