Question Number 64047 by aliesam last updated on 12/Jul/19

Commented by mathmax by abdo last updated on 12/Jul/19
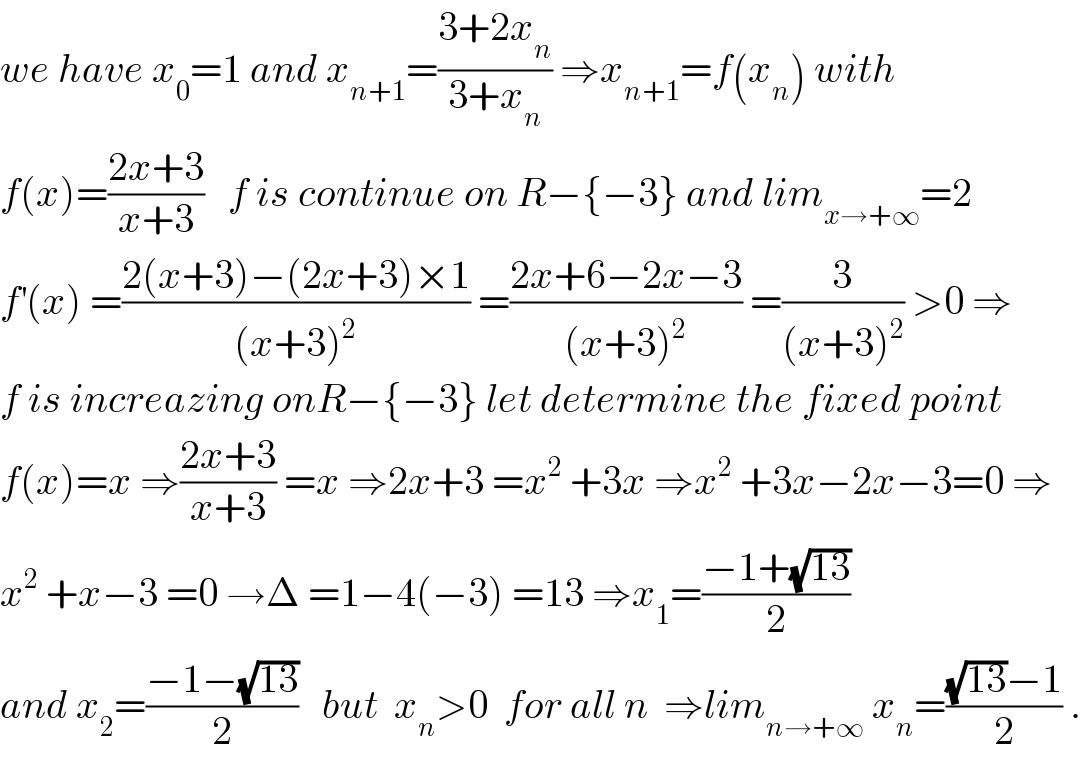
$${we}\:{have}\:{x}_{\mathrm{0}} =\mathrm{1}\:{and}\:{x}_{{n}+\mathrm{1}} =\frac{\mathrm{3}+\mathrm{2}{x}_{{n}} }{\mathrm{3}+{x}_{{n}} }\:\Rightarrow{x}_{{n}+\mathrm{1}} ={f}\left({x}_{{n}} \right)\:{with} \\ $$$${f}\left({x}\right)=\frac{\mathrm{2}{x}+\mathrm{3}}{{x}+\mathrm{3}}\:\:\:{f}\:{is}\:{continue}\:{on}\:{R}−\left\{−\mathrm{3}\right\}\:{and}\:{lim}_{{x}\rightarrow+\infty} =\mathrm{2} \\ $$$${f}^{'} \left({x}\right)\:=\frac{\mathrm{2}\left({x}+\mathrm{3}\right)−\left(\mathrm{2}{x}+\mathrm{3}\right)×\mathrm{1}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} }\:=\frac{\mathrm{2}{x}+\mathrm{6}−\mathrm{2}{x}−\mathrm{3}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} }\:=\frac{\mathrm{3}}{\left({x}+\mathrm{3}\right)^{\mathrm{2}} }\:>\mathrm{0}\:\Rightarrow \\ $$$${f}\:{is}\:{increazing}\:{onR}−\left\{−\mathrm{3}\right\}\:{let}\:{determine}\:{the}\:{fixed}\:{point} \\ $$$${f}\left({x}\right)={x}\:\Rightarrow\frac{\mathrm{2}{x}+\mathrm{3}}{{x}+\mathrm{3}}\:={x}\:\Rightarrow\mathrm{2}{x}+\mathrm{3}\:={x}^{\mathrm{2}} \:+\mathrm{3}{x}\:\Rightarrow{x}^{\mathrm{2}} \:+\mathrm{3}{x}−\mathrm{2}{x}−\mathrm{3}=\mathrm{0}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} \:+{x}−\mathrm{3}\:=\mathrm{0}\:\rightarrow\Delta\:=\mathrm{1}−\mathrm{4}\left(−\mathrm{3}\right)\:=\mathrm{13}\:\Rightarrow{x}_{\mathrm{1}} =\frac{−\mathrm{1}+\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$${and}\:{x}_{\mathrm{2}} =\frac{−\mathrm{1}−\sqrt{\mathrm{13}}}{\mathrm{2}}\:\:\:{but}\:\:{x}_{{n}} >\mathrm{0}\:\:{for}\:{all}\:{n}\:\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{x}_{{n}} =\frac{\sqrt{\mathrm{13}}−\mathrm{1}}{\mathrm{2}}\:. \\ $$
Commented by aliesam last updated on 12/Jul/19

$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 12/Jul/19
$${you}\:{are}\:{welcome}. \\ $$
