Let-f-x-x-1-2-for-all-x-1-If-g-x-is-the-function-whose-graph-is-the-reflection-of-the-graph-of-f-x-with-respect-to-the-line-y-x-then-g-x-is-equal-to-

Question Number 129622 by Ar Brandon last updated on 16/Jan/21

$$\mathrm{Let}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\mathrm{for}\:\mathrm{all}\:\mathrm{x}\geqslant−\mathrm{1}.\:\mathrm{If}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{the} \\ $$$$\mathrm{function}\:\mathrm{whose}\:\mathrm{graph}\:\mathrm{is}\:\mathrm{the}\:\mathrm{reflection}\:\mathrm{of}\:\mathrm{the}\:\mathrm{graph} \\ $$$$\mathrm{of}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{with}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{the}\:\mathrm{line}\:\mathrm{y}=\mathrm{x},\:\mathrm{then}\:\mathrm{g}\left(\mathrm{x}\right)\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to}… \\ $$

Commented by mr W last updated on 16/Jan/21

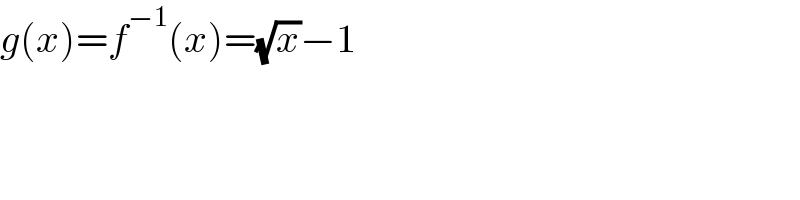
$${g}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right)=\sqrt{{x}}−\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 17/Jan/21

Thanks Sir

Answered by bemath last updated on 17/Jan/21

$$\:\begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{0}\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\mathrm{0}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:\Rightarrow\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{0}\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\mathrm{0}}\end{pmatrix}^{−\mathrm{1}} \begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix} \\ $$$$\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\frac{\mathrm{1}}{\mathrm{0}−\mathrm{1}}\:\begin{pmatrix}{\:\:\:\:\mathrm{0}\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix} \\ $$$$\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\mathrm{0}}\end{pmatrix}\begin{pmatrix}{\mathrm{x}'}\\{\mathrm{y}'}\end{pmatrix}\:\:=\begin{pmatrix}{\mathrm{y}'}\\{\mathrm{x}'}\end{pmatrix} \\ $$$$\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{y}=\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{x}'\:=\:\left(\mathrm{y}'+\mathrm{1}\right)^{\mathrm{2}} \:;\:\mathrm{y}+\mathrm{1}\:=\:\sqrt{\mathrm{x}}\:;\:\mathrm{y}\:=\:\sqrt{\mathrm{x}}\:−\mathrm{1} \\ $$$$\:\mathrm{g}\left(\mathrm{x}\right)=\sqrt{\mathrm{x}}\:−\mathrm{1}\:. \\ $$

Commented by Ar Brandon last updated on 17/Jan/21

Thanks bro

Terms of Service
Privacy Policy
Contact: info@tinkutara.com