Question Number 129719 by bramlexs22 last updated on 18/Jan/21
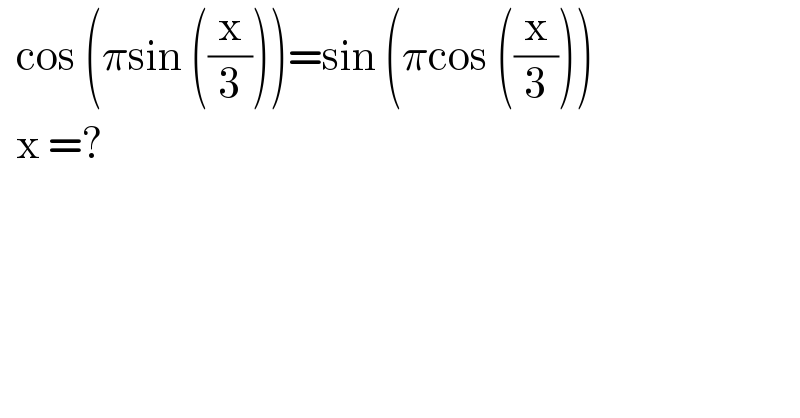
$$\:\:\mathrm{cos}\:\left(\pi\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right)=\mathrm{sin}\:\left(\pi\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right) \\ $$$$\:\:\mathrm{x}\:=? \\ $$$$ \\ $$
Answered by liberty last updated on 18/Jan/21
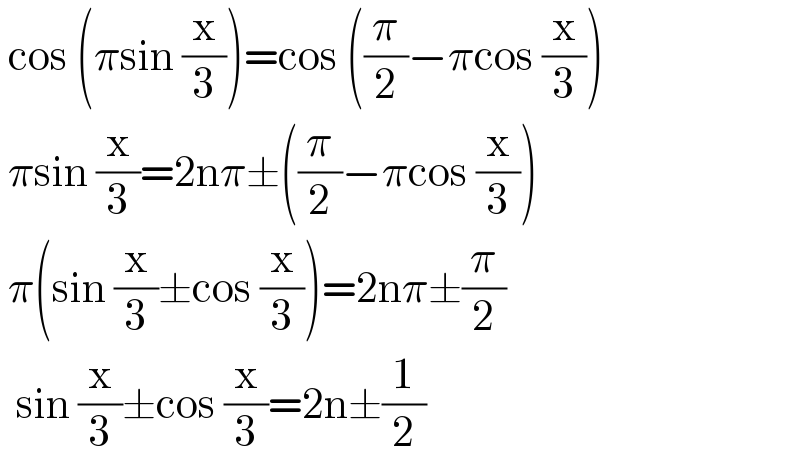
$$\:\mathrm{cos}\:\left(\pi\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{3}}\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\pi\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{3}}\right) \\ $$$$\:\pi\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{3}}=\mathrm{2n}\pi\pm\left(\frac{\pi}{\mathrm{2}}−\pi\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{3}}\right) \\ $$$$\:\pi\left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{3}}\pm\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{3}}\right)=\mathrm{2n}\pi\pm\frac{\pi}{\mathrm{2}} \\ $$$$\:\:\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{3}}\pm\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{3}}=\mathrm{2n}\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 19/Jan/21
![cos (πsin ((x/3)))=sin (πcos ((x/3))) cos (πsin ((x/3)))=cos ((π/2)−πcos ((x/3))) πsin ((x/3))=2nπ±((π/2)−πcos ((x/3))) sin ((x/3))±cos ((x/3))=2n±(π/2)−πcos ((x/3)) (√2) sin ((x/3)±(π/4))=2n±(1/2) sin ((x/3)±(π/4))=(√2)(n±(1/4)) −1≤(√2)(n±(1/4))≤1 −(1/( (√2)))∓(1/4)≤n≤(1/( (√2)))∓(1/4) −(1/( (√2)))−(1/4)≤n≤(1/( (√2)))−(1/4) ⇒n=0 −(1/( (√2)))+(1/4)≤n≤(1/( (√2)))+(1/4) ⇒n=0 sin ((x/3)±(π/4))=±((√2)/4) (x/3)±(π/4)=kπ±(−1)^k sin^(−1) ((√2)/4) ⇒x=3[kπ±(π/4)∓(−1)^k sin^(−1) ((√2)/4)]](https://www.tinkutara.com/question/Q129793.png)
$$\mathrm{cos}\:\left(\pi\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right)=\mathrm{sin}\:\left(\pi\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right) \\ $$$$\mathrm{cos}\:\left(\pi\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right)=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{2}}−\pi\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right) \\ $$$$\pi\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)=\mathrm{2}{n}\pi\pm\left(\frac{\pi}{\mathrm{2}}−\pi\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\right) \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)\pm\mathrm{cos}\:\left(\frac{{x}}{\mathrm{3}}\right)=\mathrm{2}{n}\pm\frac{\pi}{\mathrm{2}}−\pi\mathrm{cos}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right) \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\pm\frac{\pi}{\mathrm{4}}\right)=\mathrm{2}{n}\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\pm\frac{\pi}{\mathrm{4}}\right)=\sqrt{\mathrm{2}}\left({n}\pm\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$−\mathrm{1}\leqslant\sqrt{\mathrm{2}}\left({n}\pm\frac{\mathrm{1}}{\mathrm{4}}\right)\leqslant\mathrm{1} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mp\frac{\mathrm{1}}{\mathrm{4}}\leqslant{n}\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mp\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{4}}\leqslant{n}\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{n}=\mathrm{0} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{4}}\leqslant{n}\leqslant\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{n}=\mathrm{0} \\ $$$$\mathrm{sin}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\pm\frac{\pi}{\mathrm{4}}\right)=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\frac{\mathrm{x}}{\mathrm{3}}\pm\frac{\pi}{\mathrm{4}}={k}\pi\pm\left(−\mathrm{1}\right)^{{k}} \mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\mathrm{3}\left[{k}\pi\pm\frac{\pi}{\mathrm{4}}\mp\left(−\mathrm{1}\right)^{{k}} \mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\right] \\ $$
