Menu Close

As-illustrated-the-rectangle-has-an-area-of-1-and-E-is-the-midpoint-of-AD-BF-is-one-third-of-AB-What-is-the-area-of-the-shadow-

Tinku Tara 0 Comments
Pin




Question Number 137363 by liberty last updated on 02/Apr/21
As illustrated, the rectangle has an area of 1, and E is the midpoint of AD. BF is one third of AB. What is the area of the shadow?
$$ \\ $$As illustrated, the rectangle has an area of 1, and E is the midpoint of AD. BF is one third of AB. What is the area of the shadow?
Commented by liberty last updated on 02/Apr/21
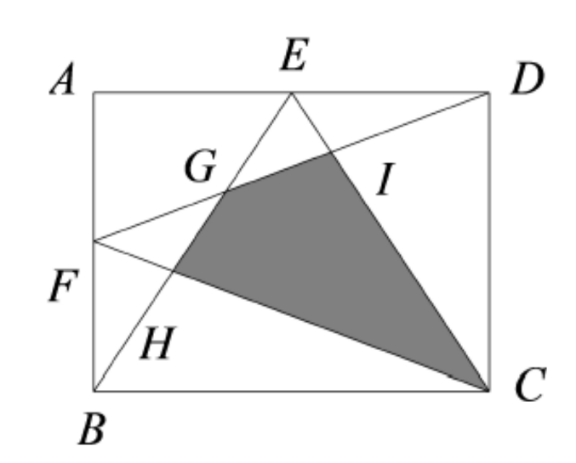
Answered by mr W last updated on 02/Apr/21
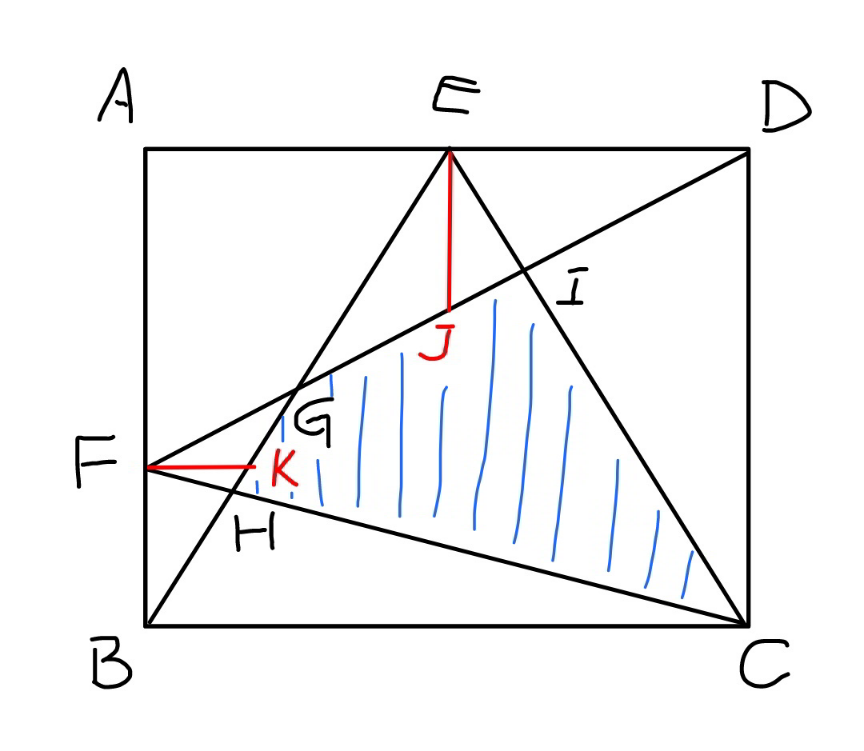
Commented by mr W last updated on 02/Apr/21
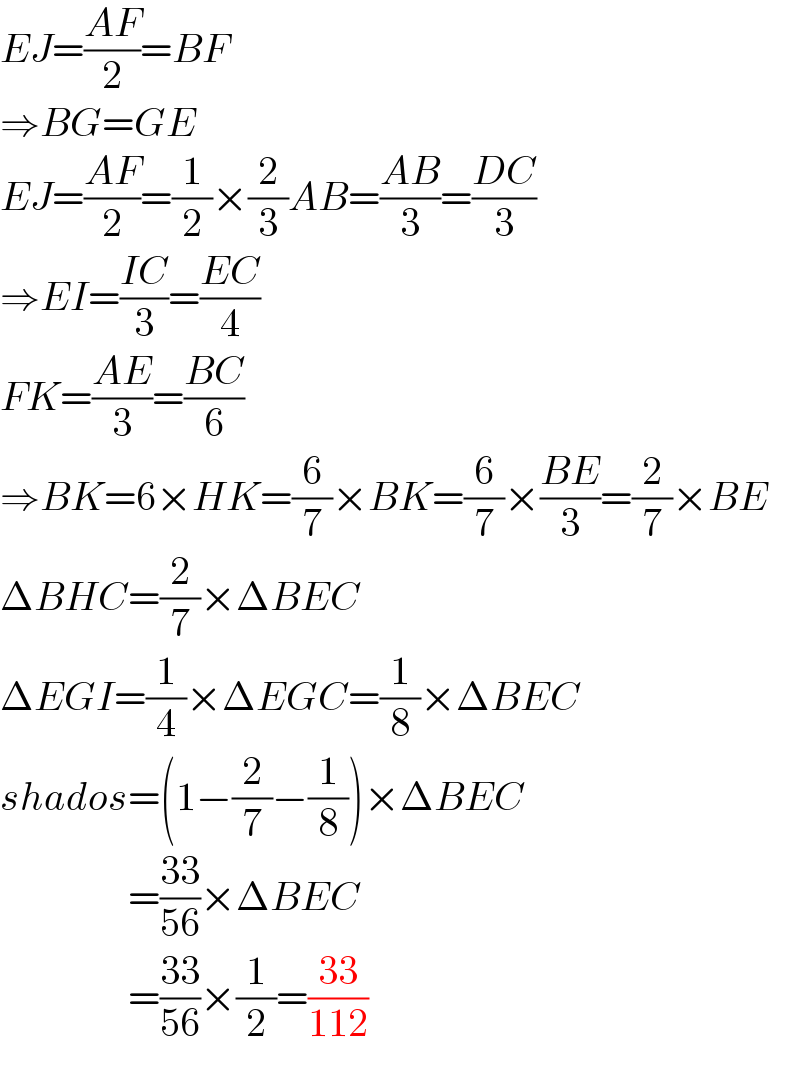
EJ=((AF)/2)=BF ⇒BG=GE EJ=((AF)/2)=(1/2)×(2/3)AB=((AB)/3)=((DC)/3) ⇒EI=((IC)/3)=((EC)/4) FK=((AE)/3)=((BC)/6) ⇒BK=6×HK=(6/7)×BK=(6/7)×((BE)/3)=(2/7)×BE ΔBHC=(2/7)×ΔBEC ΔEGI=(1/4)×ΔEGC=(1/8)×ΔBEC shados=(1−(2/7)−(1/8))×ΔBEC =((33)/(56))×ΔBEC =((33)/(56))×(1/2)=((33)/(112))
$${EJ}=\frac{{AF}}{\mathrm{2}}={BF} \\ $$$$\Rightarrow{BG}={GE} \\ $$$${EJ}=\frac{{AF}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}{AB}=\frac{{AB}}{\mathrm{3}}=\frac{{DC}}{\mathrm{3}} \\ $$$$\Rightarrow{EI}=\frac{{IC}}{\mathrm{3}}=\frac{{EC}}{\mathrm{4}} \\ $$$${FK}=\frac{{AE}}{\mathrm{3}}=\frac{{BC}}{\mathrm{6}} \\ $$$$\Rightarrow{BK}=\mathrm{6}×{HK}=\frac{\mathrm{6}}{\mathrm{7}}×{BK}=\frac{\mathrm{6}}{\mathrm{7}}×\frac{{BE}}{\mathrm{3}}=\frac{\mathrm{2}}{\mathrm{7}}×{BE} \\ $$$$\Delta{BHC}=\frac{\mathrm{2}}{\mathrm{7}}×\Delta{BEC} \\ $$$$\Delta{EGI}=\frac{\mathrm{1}}{\mathrm{4}}×\Delta{EGC}=\frac{\mathrm{1}}{\mathrm{8}}×\Delta{BEC} \\ $$$${shados}=\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{8}}\right)×\Delta{BEC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{33}}{\mathrm{56}}×\Delta{BEC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{33}}{\mathrm{56}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{33}}{\mathrm{112}} \\ $$
Answered by EDWIN88 last updated on 02/Apr/21
we can make simpler by considering this a 12×12 square with B at origin. We have to remember to divide by 12^2 at the end. We get coordinates B(0,0) ,A(0,12),F(0,4) E(6,12), D(12,12),C(12,0). we need to? calculate G,H,I. G is the meet if BE and DF ⇒ G(3,6); H(((12)/7),((24)/7)) ; I(((15)/2), 9). The shadow area is = (1/2) ∣ determinant (((12 0)),((((12)/7) ((24)/7))))+ determinant (((((12)/7) ((24)/7))),(( 3 6)))+ determinant (((3 6)),((((15)/2) 9)))+ determinant (((((15)/2) 9)),((12 0)))∣ =(1/2)∣((288)/7) + 0 −18−108 ∣ =(1/2). ((594)/7) = ((297)/7) .Therefore we get the shadow area is ((297)/(7×144)) = ((33)/(112))
$$\mathrm{we}\:\mathrm{can}\:\mathrm{make}\:\mathrm{simpler}\:\mathrm{by}\:\mathrm{considering}\:\mathrm{this} \\ $$$$\mathrm{a}\:\mathrm{12}×\mathrm{12}\:\mathrm{square}\:\mathrm{with}\:\mathrm{B}\:\mathrm{at}\:\mathrm{origin}.\:\mathrm{We}\:\mathrm{have} \\ $$$$\mathrm{to}\:\mathrm{remember}\:\mathrm{to}\:\mathrm{divide}\:\mathrm{by}\:\mathrm{12}^{\mathrm{2}} \:\mathrm{at}\:\mathrm{the}\:\mathrm{end}. \\ $$$$\mathrm{We}\:\mathrm{get}\:\mathrm{coordinates}\:\mathrm{B}\left(\mathrm{0},\mathrm{0}\right)\:,\mathrm{A}\left(\mathrm{0},\mathrm{12}\right),\mathrm{F}\left(\mathrm{0},\mathrm{4}\right) \\ $$$$\mathrm{E}\left(\mathrm{6},\mathrm{12}\right),\:\mathrm{D}\left(\mathrm{12},\mathrm{12}\right),\mathrm{C}\left(\mathrm{12},\mathrm{0}\right).\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}? \\ $$$$\mathrm{calculate}\:\mathrm{G},\mathrm{H},\mathrm{I}.\:\mathrm{G}\:\mathrm{is}\:\mathrm{the}\:\mathrm{meet}\:\mathrm{if}\:\mathrm{BE}\:\mathrm{and}\:\mathrm{DF} \\ $$$$\:\Rightarrow\:\mathrm{G}\left(\mathrm{3},\mathrm{6}\right);\:\mathrm{H}\left(\frac{\mathrm{12}}{\mathrm{7}},\frac{\mathrm{24}}{\mathrm{7}}\right)\:;\:\mathrm{I}\left(\frac{\mathrm{15}}{\mathrm{2}},\:\mathrm{9}\right).\: \\ $$$$\mathrm{The}\:\mathrm{shadow}\:\mathrm{area}\:\mathrm{is}\: \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\mid\:\begin{vmatrix}{\mathrm{12}\:\:\:\:\mathrm{0}}\\{\frac{\mathrm{12}}{\mathrm{7}}\:\:\:\:\frac{\mathrm{24}}{\mathrm{7}}}\end{vmatrix}+\begin{vmatrix}{\frac{\mathrm{12}}{\mathrm{7}}\:\:\:\:\frac{\mathrm{24}}{\mathrm{7}}}\\{\:\mathrm{3}\:\:\:\:\:\:\:\mathrm{6}}\end{vmatrix}+\begin{vmatrix}{\mathrm{3}\:\:\:\:\mathrm{6}}\\{\frac{\mathrm{15}}{\mathrm{2}}\:\:\mathrm{9}}\end{vmatrix}+\begin{vmatrix}{\frac{\mathrm{15}}{\mathrm{2}}\:\:\:\mathrm{9}}\\{\mathrm{12}\:\:\:\mathrm{0}}\end{vmatrix}\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mid\frac{\mathrm{288}}{\mathrm{7}}\:+\:\mathrm{0}\:−\mathrm{18}−\mathrm{108}\:\mid \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\:\frac{\mathrm{594}}{\mathrm{7}}\:=\:\frac{\mathrm{297}}{\mathrm{7}}\:.\mathrm{Therefore}\:\mathrm{we}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{shadow}\:\mathrm{area}\:\mathrm{is}\:\frac{\mathrm{297}}{\mathrm{7}×\mathrm{144}}\:=\:\frac{\mathrm{33}}{\mathrm{112}}\: \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *