Menu Close

Question-64289

Tinku Tara 0 Comments
Pin




Question Number 64289 by ajfour last updated on 16/Jul/19
Commented by ajfour last updated on 16/Jul/19
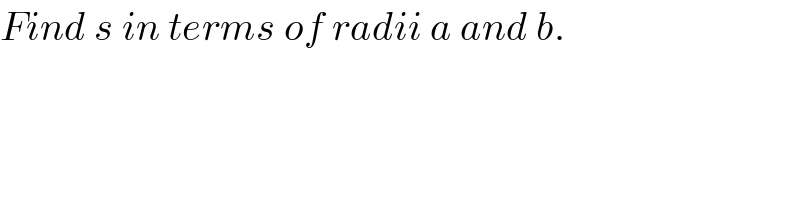
Find s in terms of radii a and b.
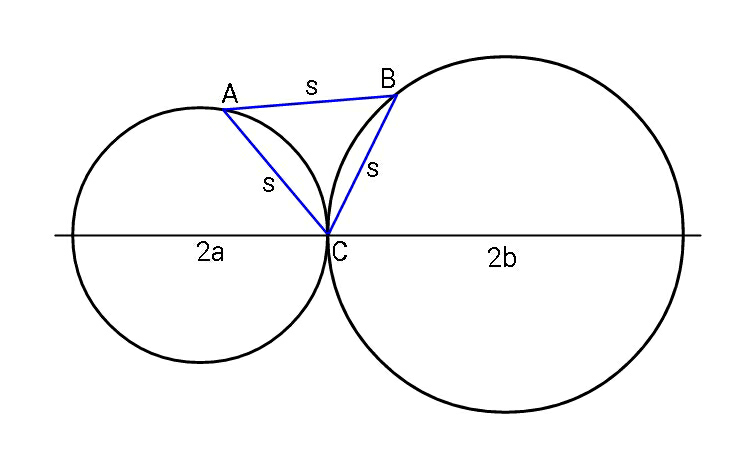
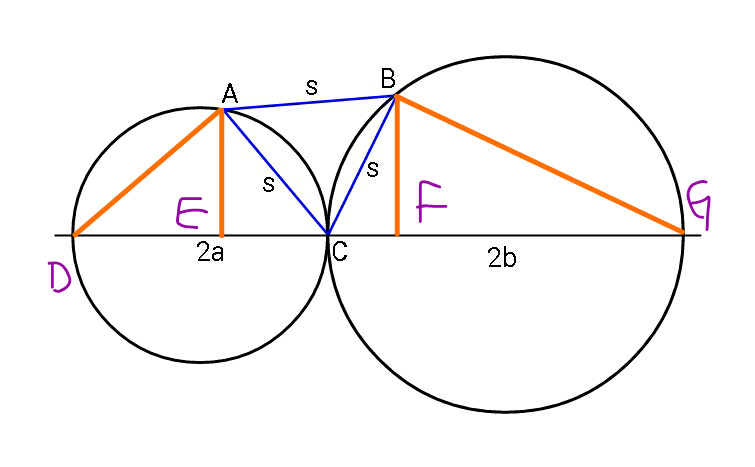
$${Find}\:{s}\:{in}\:{terms}\:{of}\:{radii}\:{a}\:{and}\:{b}. \\ $$
Commented by behi83417@gmail.com last updated on 16/Jul/19
.
$$. \\ $$
Answered by mr W last updated on 16/Jul/19
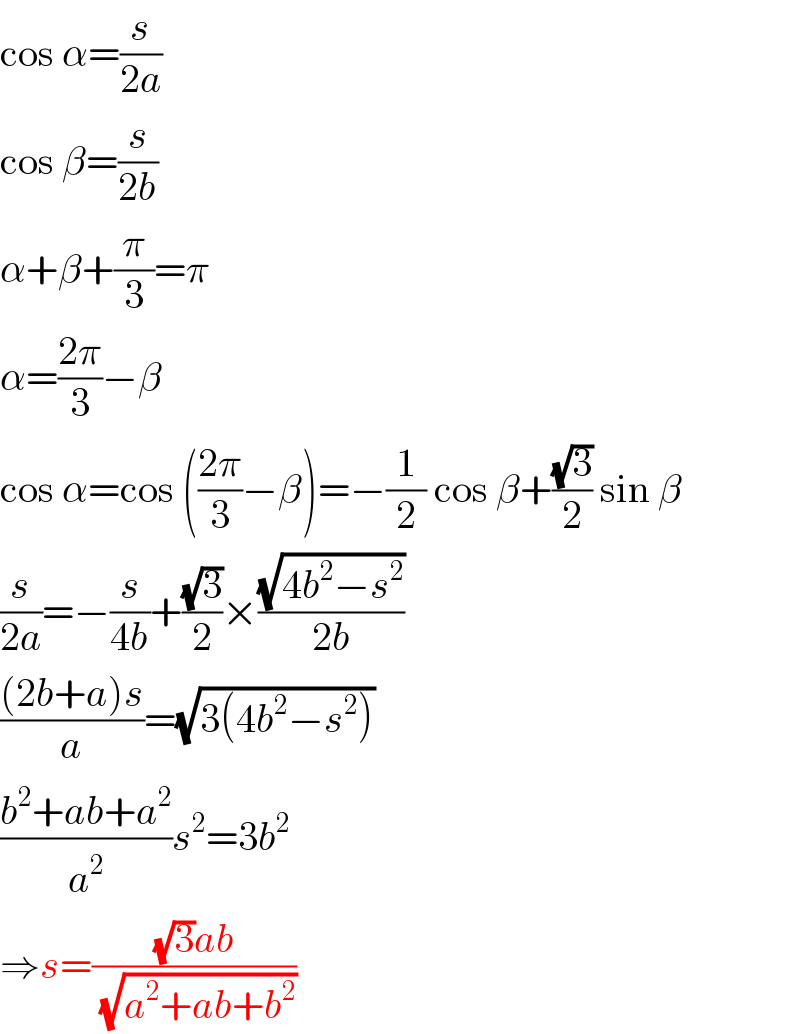
cos α=(s/(2a)) cos β=(s/(2b)) α+β+(π/3)=π α=((2π)/3)−β cos α=cos (((2π)/3)−β)=−(1/2) cos β+((√3)/2) sin β (s/(2a))=−(s/(4b))+((√3)/2)×((√(4b^2 −s^2 ))/(2b)) (((2b+a)s)/a)=(√(3(4b^2 −s^2 ))) ((b^2 +ab+a^2 )/a^2 )s^2 =3b^2 ⇒s=(((√3)ab)/( (√(a^2 +ab+b^2 ))))
$$\mathrm{cos}\:\alpha=\frac{{s}}{\mathrm{2}{a}} \\ $$$$\mathrm{cos}\:\beta=\frac{{s}}{\mathrm{2}{b}} \\ $$$$\alpha+\beta+\frac{\pi}{\mathrm{3}}=\pi \\ $$$$\alpha=\frac{\mathrm{2}\pi}{\mathrm{3}}−\beta \\ $$$$\mathrm{cos}\:\alpha=\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\beta\right)=−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\beta+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{sin}\:\beta \\ $$$$\frac{{s}}{\mathrm{2}{a}}=−\frac{{s}}{\mathrm{4}{b}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{4}{b}^{\mathrm{2}} −{s}^{\mathrm{2}} }}{\mathrm{2}{b}} \\ $$$$\frac{\left(\mathrm{2}{b}+{a}\right){s}}{{a}}=\sqrt{\mathrm{3}\left(\mathrm{4}{b}^{\mathrm{2}} −{s}^{\mathrm{2}} \right)} \\ $$$$\frac{{b}^{\mathrm{2}} +{ab}+{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} }{s}^{\mathrm{2}} =\mathrm{3}{b}^{\mathrm{2}} \\ $$$$\Rightarrow{s}=\frac{\sqrt{\mathrm{3}}{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }} \\ $$
Commented by ajfour last updated on 17/Jul/19
thank you sir.
$${thank}\:{you}\:{sir}. \\ $$
Commented by Tawa1 last updated on 17/Jul/19
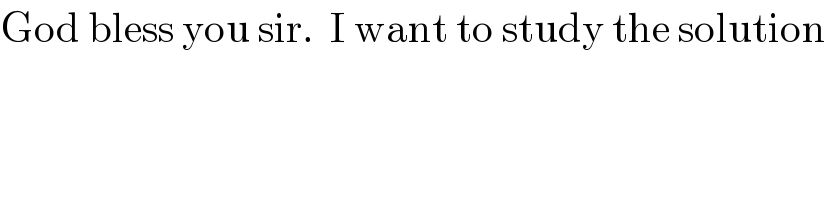
God bless you sir. I want to study the solution
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\:\mathrm{I}\:\mathrm{want}\:\mathrm{to}\:\mathrm{study}\:\mathrm{the}\:\mathrm{solution} \\ $$
Answered by mr W last updated on 17/Jul/19
Commented by mr W last updated on 17/Jul/19
((EC)/(AC))=((AC)/(DC)) ⇒EC=(s^2 /(2a)) AE^2 =AC^2 −EC^2 =s^2 −(s^4 /(4a^2 )) similarly CF=(s^2 /(2b)) BF^2 =s^2 −(s^4 /(4b^2 )) AB^2 =(EC+CF)^2 +(BF−AE)^2 s^2 =((s^2 /(2a))+(s^2 /(2b)))^2 +s^2 −(s^4 /(4a^2 ))+s^2 −(s^4 /(4b^2 ))−2(√((s^2 −(s^4 /(4a^2 )))(s^2 −(s^4 /(4b^2 ))))) (s^4 /(2ab))+s^2 =2(√((s^2 −(s^4 /(4a^2 )))(s^2 −(s^4 /(4b^2 ))))) (s^2 /(2ab))+1=2(√((1−(s^2 /(4a^2 )))(1−(s^2 /(4b^2 ))))) ((s^2 /(2ab))+1)^2 =4(1−(s^2 /(4a^2 )))(1−(s^2 /(4b^2 ))) (s^4 /(4a^2 b^2 ))+1+(s^2 /(ab))=4(1−(s^2 /(4a^2 ))−(s^2 /(4b^2 ))+(s^4 /(16a^2 b^2 ))) (s^2 /(ab))=3−(s^2 /a^2 )−(s^2 /b^2 ) ((1/a^2 )+(1/(ab))+(1/b^2 ))s^2 =3 (a^2 +ab+b^2 )s^2 =3a^2 b^2 ⇒s=(((√3)ab)/( (√(a^2 +ab+b^2 ))))
$$\frac{{EC}}{{AC}}=\frac{{AC}}{{DC}} \\ $$$$\Rightarrow{EC}=\frac{{s}^{\mathrm{2}} }{\mathrm{2}{a}} \\ $$$${AE}^{\mathrm{2}} ={AC}^{\mathrm{2}} −{EC}^{\mathrm{2}} ={s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{a}^{\mathrm{2}} } \\ $$$${similarly} \\ $$$${CF}=\frac{{s}^{\mathrm{2}} }{\mathrm{2}{b}} \\ $$$${BF}^{\mathrm{2}} ={s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{b}^{\mathrm{2}} } \\ $$$${AB}^{\mathrm{2}} =\left({EC}+{CF}\right)^{\mathrm{2}} +\left({BF}−{AE}\right)^{\mathrm{2}} \\ $$$${s}^{\mathrm{2}} =\left(\frac{{s}^{\mathrm{2}} }{\mathrm{2}{a}}+\frac{{s}^{\mathrm{2}} }{\mathrm{2}{b}}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{a}^{\mathrm{2}} }+{s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{b}^{\mathrm{2}} }−\mathrm{2}\sqrt{\left({s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)\left({s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{b}^{\mathrm{2}} }\right)} \\ $$$$\frac{{s}^{\mathrm{4}} }{\mathrm{2}{ab}}+{s}^{\mathrm{2}} =\mathrm{2}\sqrt{\left({s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)\left({s}^{\mathrm{2}} −\frac{{s}^{\mathrm{4}} }{\mathrm{4}{b}^{\mathrm{2}} }\right)} \\ $$$$\frac{{s}^{\mathrm{2}} }{\mathrm{2}{ab}}+\mathrm{1}=\mathrm{2}\sqrt{\left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }\right)} \\ $$$$\left(\frac{{s}^{\mathrm{2}} }{\mathrm{2}{ab}}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }\right) \\ $$$$\frac{{s}^{\mathrm{4}} }{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }+\mathrm{1}+\frac{{s}^{\mathrm{2}} }{{ab}}=\mathrm{4}\left(\mathrm{1}−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{a}^{\mathrm{2}} }−\frac{{s}^{\mathrm{2}} }{\mathrm{4}{b}^{\mathrm{2}} }+\frac{{s}^{\mathrm{4}} }{\mathrm{16}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right) \\ $$$$\frac{{s}^{\mathrm{2}} }{{ab}}=\mathrm{3}−\frac{{s}^{\mathrm{2}} }{{a}^{\mathrm{2}} }−\frac{{s}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{ab}}+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right){s}^{\mathrm{2}} =\mathrm{3} \\ $$$$\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right){s}^{\mathrm{2}} =\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \\ $$$$\Rightarrow{s}=\frac{\sqrt{\mathrm{3}}{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} }} \\ $$
Commented by Tawa1 last updated on 18/Jul/19
I appreciate your effort sir. God bless you more
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{effort}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *