Question Number 129868 by Bird last updated on 20/Jan/21
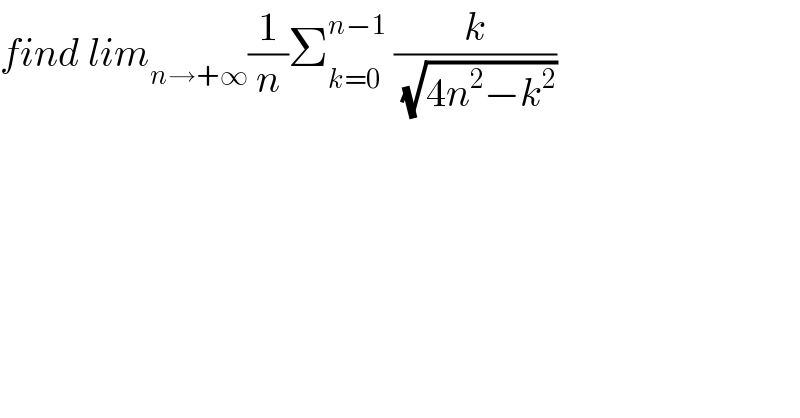
$${find}\:{lim}_{{n}\rightarrow+\infty} \frac{\mathrm{1}}{{n}}\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{k}}{\:\sqrt{\mathrm{4}{n}^{\mathrm{2}} −{k}^{\mathrm{2}} }} \\ $$
Answered by Ar Brandon last updated on 20/Jan/21
![S_∞ =lim_(n→∞) (1/n)Σ_(k=0) ^(n−1) (k/(n(√(4−(k^2 /n^2 ))))) =∫_0 ^1 (x/( (√(4−x^2 ))))dx=[−(√(4−x^2 ))]_0 ^1 =2−(√3)](https://www.tinkutara.com/question/Q129891.png)
$$\mathrm{S}_{\infty} =\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}−\mathrm{1}} {\sum}}\frac{\mathrm{k}}{\mathrm{n}\sqrt{\mathrm{4}−\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }}} \\ $$$$\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}}{\:\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}=\left[−\sqrt{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$
