Menu Close

dx-sin-3-xcos-5-x-

Tinku Tara 0 Comments
Pin




Question Number 129907 by pticantor last updated on 20/Jan/21
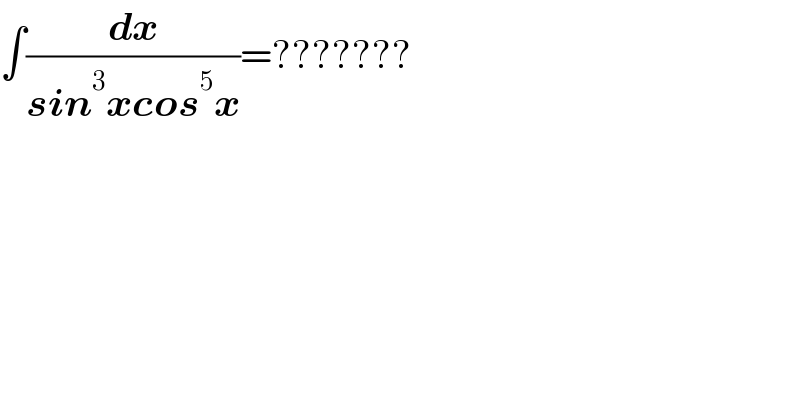
∫(dx/(sin^3 xcos^5 x))=???????
$$\int\frac{\boldsymbol{{dx}}}{\boldsymbol{{sin}}^{\mathrm{3}} \boldsymbol{{xcos}}^{\mathrm{5}} \boldsymbol{{x}}}=??????? \\ $$
Answered by Ar Brandon last updated on 20/Jan/21
I=∫(dx/(sin^3 xcos^5 x))=∫((cos^2 x+sin^2 x)/(sin^3 xcos^5 x))dx =∫{(1/(sin^3 xcos^3 x))+(1/(sinxcos^5 x))}dx=∫{((cos^2 x+sin^2 x)/(sin^3 xcos^3 x))+((cos^2 x+sin^2 x)/(sinxcos^5 x))}dx =∫{(1/(sin^3 xcosx))+(1/(sinxcos^3 x))+(1/(sinxcos^3 x))+((sinx)/(cos^5 x))}dx =∫{((cosx)/(sin^3 x))+(1/(sinxcosx))+(1/(sinxcosx))+((sinx)/(cos^3 x))+(1/(sinxcosx))+((sinx)/(cos^3 x))+((sinx)/(cos^5 x))}dx =∫{((cosx)/(sin^3 x))+2∙((sinx)/(cos^3 x))+((sinx)/(cos^5 x))+3∙((cos^2 x+sin^2 x)/(sinxcosx))}dx =∫{((cosx)/(sin^3 x))+2∙((sinx)/(cos^3 x))+((sinx)/(cos^5 x))+3∙((cosx)/(sinx))+3∙((sinx)/(cosx))}dx =−(1/(3sin^2 x))+(1/(cos^2 x))+(1/(4cos^4 x))+3ln∣tanx∣+C
$$\mathcal{I}=\int\frac{\mathrm{dx}}{\mathrm{sin}^{\mathrm{3}} \mathrm{xcos}^{\mathrm{5}} \mathrm{x}}=\int\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{3}} \mathrm{xcos}^{\mathrm{5}} \mathrm{x}}\mathrm{dx} \\ $$$$\:\:\:=\int\left\{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{3}} \mathrm{xcos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{sinxcos}^{\mathrm{5}} \mathrm{x}}\right\}\mathrm{dx}=\int\left\{\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{3}} \mathrm{xcos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinxcos}^{\mathrm{5}} \mathrm{x}}\right\}\mathrm{dx} \\ $$$$\:\:\:=\int\left\{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{3}} \mathrm{xcosx}}+\frac{\mathrm{1}}{\mathrm{sinxcos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{sinxcos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{5}} \mathrm{x}}\right\}\mathrm{dx} \\ $$$$\:\:\:=\int\left\{\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{sinxcosx}}+\frac{\mathrm{1}}{\mathrm{sinxcosx}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{sinxcosx}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{5}} \mathrm{x}}\right\}\mathrm{dx} \\ $$$$\:\:\:=\int\left\{\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}+\mathrm{2}\centerdot\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{5}} \mathrm{x}}+\mathrm{3}\centerdot\frac{\mathrm{cos}^{\mathrm{2}} \mathrm{x}+\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{sinxcosx}}\right\}\mathrm{dx} \\ $$$$\:\:\:=\int\left\{\frac{\mathrm{cosx}}{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}+\mathrm{2}\centerdot\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{3}} \mathrm{x}}+\frac{\mathrm{sinx}}{\mathrm{cos}^{\mathrm{5}} \mathrm{x}}+\mathrm{3}\centerdot\frac{\mathrm{cosx}}{\mathrm{sinx}}+\mathrm{3}\centerdot\frac{\mathrm{sinx}}{\mathrm{cosx}}\right\}\mathrm{dx} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{3sin}^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}+\frac{\mathrm{1}}{\mathrm{4cos}^{\mathrm{4}} \mathrm{x}}+\mathrm{3ln}\mid\mathrm{tanx}\mid+\mathcal{C} \\ $$
Answered by MJS_new last updated on 20/Jan/21
∫(dx/(sin^3 x cos^5 x))=∫(((1+tan^2 x)^4 )/(tan^3 x))dx= [t=tan x → dx=(dt/(1+t^2 ))] =∫(((t^2 +1)^3 )/t^3 )dt=∫(t^3 +3t+(3/t)+(1/t^3 ))dt= =(1/4)t^4 +(3/2)t^2 +3ln t −(1/(2t^2 ))= =((tan^6 x +6tan^4 x −2)/(4tan^2 x))+3ln ∣tan x∣ +C
$$\int\frac{{dx}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:\mathrm{cos}^{\mathrm{5}} \:{x}}=\int\frac{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:{x}\right)^{\mathrm{4}} }{\mathrm{tan}^{\mathrm{3}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right] \\ $$$$=\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{{t}^{\mathrm{3}} }{dt}=\int\left({t}^{\mathrm{3}} +\mathrm{3}{t}+\frac{\mathrm{3}}{{t}}+\frac{\mathrm{1}}{{t}^{\mathrm{3}} }\right){dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{t}^{\mathrm{4}} +\frac{\mathrm{3}}{\mathrm{2}}{t}^{\mathrm{2}} +\mathrm{3ln}\:{t}\:−\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{2}} }= \\ $$$$=\frac{\mathrm{tan}^{\mathrm{6}} \:{x}\:+\mathrm{6tan}^{\mathrm{4}} \:{x}\:−\mathrm{2}}{\mathrm{4tan}^{\mathrm{2}} \:{x}}+\mathrm{3ln}\:\mid\mathrm{tan}\:{x}\mid\:+{C} \\ $$
Commented by Ar Brandon last updated on 20/Jan/21
wow ��
Commented by MJS_new last updated on 21/Jan/21
btw there seem to be questions of many different degrees. I would recommend to use the following new notation: [question∨term (=)]?^n with n∈N^★ instead of the old notation: [question∨term(=)]???...?_(n times) because it′s hard to tell i.e. ∫e^x^2 dx=??????????? from ∫e^x^2 dx=???????????? but easy to tell i.e. ∫x^x^x dx=?^(31) from ∫x^x^x dx=?^(32) , not to talk about i.e. ∫(ln x)^(sin x^x ) dx=?^(4711) which is a nightmare in the old notation. another suggestion: simply use ?^(+∞) for questions which only God is able to answer and ?^(−∞) for the silly ones. thank you
$$\mathrm{btw}\:\mathrm{there}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{be}\:\mathrm{questions}\:\mathrm{of}\:\mathrm{many} \\ $$$$\mathrm{different}\:\mathrm{degrees}.\:\mathrm{I}\:\mathrm{would}\:\mathrm{recommend}\:\mathrm{to} \\ $$$$\mathrm{use}\:\mathrm{the}\:\mathrm{following}\:{new}\:\mathrm{notation}: \\ $$$$\left[{question}\vee{term}\:\left(=\right)\right]?^{{n}} \:\mathrm{with}\:{n}\in\mathbb{N}^{\bigstar} \:\mathrm{instead} \\ $$$$\mathrm{of}\:\mathrm{the}\:{old}\:\mathrm{notation}: \\ $$$$\left[{question}\vee{term}\left(=\right)\right]\underset{{n}\:{times}} {???…?}\:\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{hard} \\ $$$$\mathrm{to}\:\mathrm{tell}\:\mathrm{i}.\mathrm{e}.\:\int\mathrm{e}^{{x}^{\mathrm{2}} } {dx}=???????????\:\mathrm{from} \\ $$$$\int\mathrm{e}^{{x}^{\mathrm{2}} } {dx}=????????????\:\mathrm{but}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{tell} \\ $$$$\mathrm{i}.\mathrm{e}.\:\int{x}^{{x}^{{x}} } {dx}=?^{\mathrm{31}} \:\mathrm{from}\:\int{x}^{{x}^{{x}} } {dx}=?^{\mathrm{32}} ,\:\mathrm{not}\:\mathrm{to} \\ $$$$\mathrm{talk}\:\mathrm{about}\:\mathrm{i}.\mathrm{e}.\:\int\left(\mathrm{ln}\:{x}\right)^{\mathrm{sin}\:{x}^{{x}} } {dx}=?^{\mathrm{4711}} \:\mathrm{which} \\ $$$$\mathrm{is}\:\mathrm{a}\:\mathrm{nightmare}\:\mathrm{in}\:\mathrm{the}\:{old}\:\mathrm{notation}. \\ $$$$\mathrm{another}\:\mathrm{suggestion}:\:\mathrm{simply}\:\mathrm{use}\:?^{+\infty} \:\mathrm{for} \\ $$$$\mathrm{questions}\:\mathrm{which}\:\mathrm{only}\:\mathrm{God}\:\mathrm{is}\:\mathrm{able}\:\mathrm{to}\:\mathrm{answer} \\ $$$$\mathrm{and}\:?^{−\infty} \:\mathrm{for}\:\mathrm{the}\:\mathrm{silly}\:\mathrm{ones}. \\ $$$$\mathrm{thank}\:\mathrm{you} \\ $$
Commented by $@y@m last updated on 21/Jan/21
������
Answered by bemath last updated on 21/Jan/21
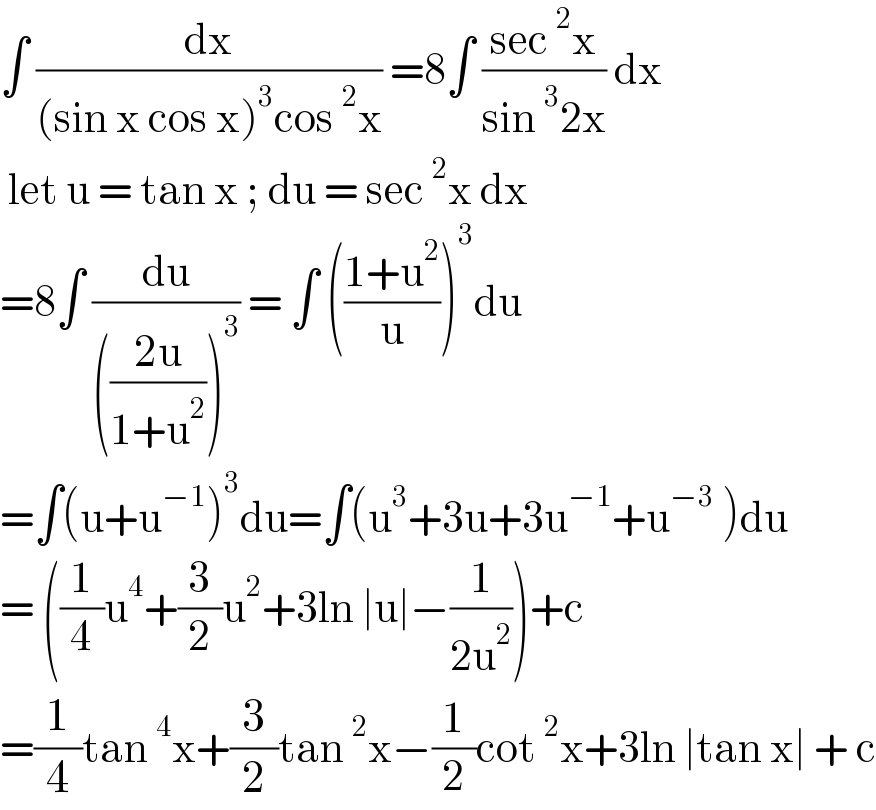
∫ (dx/((sin x cos x)^3 cos^2 x)) =8∫ ((sec^2 x)/(sin^3 2x)) dx let u = tan x ; du = sec^2 x dx =8∫ (du/((((2u)/(1+u^2 )))^3 )) = ∫ (((1+u^2 )/u))^3 du =∫(u+u^(−1) )^3 du=∫(u^3 +3u+3u^(−1) +u^(−3) )du = ((1/4)u^4 +(3/2)u^2 +3ln ∣u∣−(1/(2u^2 )))+c =(1/4)tan^4 x+(3/2)tan^2 x−(1/2)cot^2 x+3ln ∣tan x∣ + c
$$\int\:\frac{\mathrm{dx}}{\left(\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}\right)^{\mathrm{3}} \mathrm{cos}\:^{\mathrm{2}} \mathrm{x}}\:=\mathrm{8}\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}\:^{\mathrm{3}} \mathrm{2x}}\:\mathrm{dx} \\ $$$$\:\mathrm{let}\:\mathrm{u}\:=\:\mathrm{tan}\:\mathrm{x}\:;\:\mathrm{du}\:=\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}\:\mathrm{dx}\: \\ $$$$=\mathrm{8}\int\:\frac{\mathrm{du}}{\left(\frac{\mathrm{2u}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\right)^{\mathrm{3}} }\:=\:\int\:\left(\frac{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }{\mathrm{u}}\right)^{\mathrm{3}} \mathrm{du}\: \\ $$$$=\int\left(\mathrm{u}+\mathrm{u}^{−\mathrm{1}} \right)^{\mathrm{3}} \mathrm{du}=\int\left(\mathrm{u}^{\mathrm{3}} +\mathrm{3u}+\mathrm{3u}^{−\mathrm{1}} +\mathrm{u}^{−\mathrm{3}} \:\right)\mathrm{du} \\ $$$$=\:\left(\frac{\mathrm{1}}{\mathrm{4}}\mathrm{u}^{\mathrm{4}} +\frac{\mathrm{3}}{\mathrm{2}}\mathrm{u}^{\mathrm{2}} +\mathrm{3ln}\:\mid\mathrm{u}\mid−\frac{\mathrm{1}}{\mathrm{2u}^{\mathrm{2}} }\right)+\mathrm{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{tan}\:^{\mathrm{4}} \mathrm{x}+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} \mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cot}\:^{\mathrm{2}} \mathrm{x}+\mathrm{3ln}\:\mid\mathrm{tan}\:\mathrm{x}\mid\:+\:\mathrm{c} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *