Question Number 64436 by ajfour last updated on 17/Jul/19
Commented by ajfour last updated on 17/Jul/19
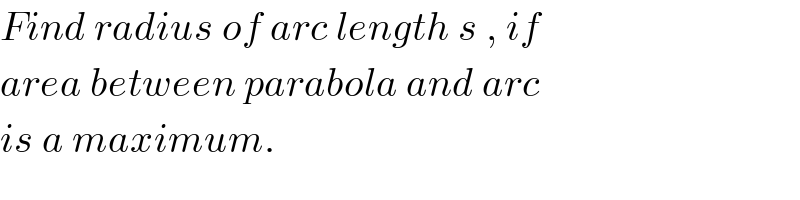
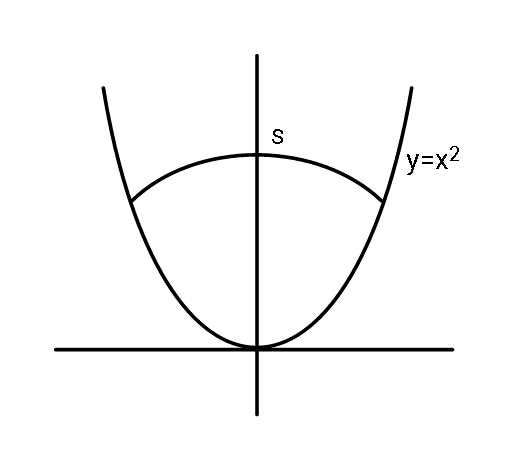
$${Find}\:{radius}\:{of}\:{arc}\:{length}\:{s}\:,\:{if} \\ $$$${area}\:{between}\:{parabola}\:{and}\:{arc} \\ $$$${is}\:{a}\:{maximum}. \\ $$
Answered by Tanmay chaudhury last updated on 18/Jul/19
![y=x^2 curve passes through (α,α^2 ) and (−α,α^2 ) arc is a portion of circle ...that circle pass through(α,α^2 ) ,(−α,α^2 ) and (0,β) x^2 +y^2 +2gx+2fy+c=0 α^2 +α^4 +2gα+2fα^2 +c=0 α^2 +α^4 −2gα+2fα^2 +c=0 β^2 +2fβ+c=0 4gα=0 g=0 α^2 +α^4 +2fα^2 +c=0 β^2 +2fβ+c=0 2f(α^2 −β)+α^2 +α^4 −β^2 =0 f=((β^2 −α^2 −α^4 )/(2(α^2 −β))) β^2 +(((β^2 −α^2 −α^4 )/(α^2 −β)))β+c=0 ((α^2 β^2 −β^3 +β^3 −β(α^2 +α^4 ))/(α^2 −β))+c=0 ((α^2 β(β−1−α^2 ))/(α^2 −β))+c=0 c=((α^2 β(1+α^2 −β))/(α^2 −β)) eqn of circle x^2 +y^2 +2(((β^2 −α^2 −α^4 )/(2(α^2 −β))))y+((α^2 β(1+α^2 −β))/(α^2 −β))=0 x^2 +y^2 +2Py+Q=0 Radius=(√(P^2 −Q)) y^2 +2Py+P^2 +Q+x^2 =P^2 (y+P)^2 =P^2 −Q−x^2 y=−P+(√(P^2 −Q−x^2 )) required area which to maximise 2[∫_0 ^α^2 [(−P+(√(P^2 −Q−x^2 )) )−x^2 ] dx 2∣Px−(x^3 /3)+(x/2)(√(P^2 −Q−x^2 )) +((P^2 −Q)/2)sin^(−1) ((x/( (√(P^2 −Q)))))∣_0 ^α^2 2[Pα^2 −(α^6 /3)+(α^2 /2)(√(P^2 −Q−α^4 )) +((P^2 −Q)/2)sin^(−1) ((α^2 /( (√(P^2 −Q))))) pls check upto this ...nxt step put P and Q maximize area then finally R](https://www.tinkutara.com/question/Q64457.png)
$${y}={x}^{\mathrm{2}} \:{curve}\:{passes}\:{through}\:\left(\alpha,\alpha^{\mathrm{2}} \right)\:{and}\:\left(−\alpha,\alpha^{\mathrm{2}} \right) \\ $$$${arc}\:{is}\:{a}\:{portion}\:{of}\:{circle}\:…{that}\:{circle}\:{pass} \\ $$$${through}\left(\alpha,\alpha^{\mathrm{2}} \right)\:,\left(−\alpha,\alpha^{\mathrm{2}} \right)\:{and}\:\left(\mathrm{0},\beta\right) \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{gx}+\mathrm{2}{fy}+{c}=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\alpha^{\mathrm{4}} +\mathrm{2}{g}\alpha+\mathrm{2}{f}\alpha^{\mathrm{2}} +{c}=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\alpha^{\mathrm{4}} −\mathrm{2}{g}\alpha+\mathrm{2}{f}\alpha^{\mathrm{2}} +{c}=\mathrm{0} \\ $$$$\beta^{\mathrm{2}} +\mathrm{2}{f}\beta+{c}=\mathrm{0} \\ $$$$\mathrm{4}{g}\alpha=\mathrm{0}\:\:{g}=\mathrm{0} \\ $$$$\alpha^{\mathrm{2}} +\alpha^{\mathrm{4}} +\mathrm{2}{f}\alpha^{\mathrm{2}} +{c}=\mathrm{0} \\ $$$$\beta^{\mathrm{2}} +\mathrm{2}{f}\beta+{c}=\mathrm{0} \\ $$$$\mathrm{2}{f}\left(\alpha^{\mathrm{2}} −\beta\right)+\alpha^{\mathrm{2}} +\alpha^{\mathrm{4}} −\beta^{\mathrm{2}} =\mathrm{0} \\ $$$${f}=\frac{\beta^{\mathrm{2}} −\alpha^{\mathrm{2}} −\alpha^{\mathrm{4}} }{\mathrm{2}\left(\alpha^{\mathrm{2}} −\beta\right)} \\ $$$$\beta^{\mathrm{2}} +\left(\frac{\beta^{\mathrm{2}} −\alpha^{\mathrm{2}} −\alpha^{\mathrm{4}} }{\alpha^{\mathrm{2}} −\beta}\right)\beta+{c}=\mathrm{0} \\ $$$$\frac{\alpha^{\mathrm{2}} \beta^{\mathrm{2}} −\beta^{\mathrm{3}} +\beta^{\mathrm{3}} −\beta\left(\alpha^{\mathrm{2}} +\alpha^{\mathrm{4}} \right)}{\alpha^{\mathrm{2}} −\beta}+{c}=\mathrm{0} \\ $$$$\frac{\alpha^{\mathrm{2}} \beta\left(\beta−\mathrm{1}−\alpha^{\mathrm{2}} \right)}{\alpha^{\mathrm{2}} −\beta}+{c}=\mathrm{0} \\ $$$${c}=\frac{\alpha^{\mathrm{2}} \beta\left(\mathrm{1}+\alpha^{\mathrm{2}} −\beta\right)}{\alpha^{\mathrm{2}} −\beta} \\ $$$${eqn}\:{of}\:{circle} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}\left(\frac{\beta^{\mathrm{2}} −\alpha^{\mathrm{2}} −\alpha^{\mathrm{4}} }{\mathrm{2}\left(\alpha^{\mathrm{2}} −\beta\right)}\right){y}+\frac{\alpha^{\mathrm{2}} \beta\left(\mathrm{1}+\alpha^{\mathrm{2}} −\beta\right)}{\alpha^{\mathrm{2}} −\beta}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{Py}+{Q}=\mathrm{0} \\ $$$${Radius}=\sqrt{{P}^{\mathrm{2}} −{Q}}\: \\ $$$${y}^{\mathrm{2}} +\mathrm{2}{Py}+{P}^{\mathrm{2}} +{Q}+{x}^{\mathrm{2}} ={P}^{\mathrm{2}} \\ $$$$\left({y}+{P}\right)^{\mathrm{2}} ={P}^{\mathrm{2}} −{Q}−{x}^{\mathrm{2}} \\ $$$${y}=−{P}+\sqrt{{P}^{\mathrm{2}} −{Q}−{x}^{\mathrm{2}} }\: \\ $$$${required}\:{area}\:{which}\:{to}\:{maximise} \\ $$$$\mathrm{2}\left[\int_{\mathrm{0}} ^{\alpha^{\mathrm{2}} } \left[\left(−{P}+\sqrt{{P}^{\mathrm{2}} −{Q}−{x}^{\mathrm{2}} }\:\right)−{x}^{\mathrm{2}} \right]\:{dx}\right. \\ $$$$\mathrm{2}\mid{Px}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}}{\mathrm{2}}\sqrt{{P}^{\mathrm{2}} −{Q}−{x}^{\mathrm{2}} }\:+\frac{{P}^{\mathrm{2}} −{Q}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{{x}}{\:\sqrt{{P}^{\mathrm{2}} −{Q}}}\right)\mid_{\mathrm{0}} ^{\alpha^{\mathrm{2}} } \\ $$$$\mathrm{2}\left[{P}\alpha^{\mathrm{2}} −\frac{\alpha^{\mathrm{6}} }{\mathrm{3}}+\frac{\alpha^{\mathrm{2}} }{\mathrm{2}}\sqrt{{P}^{\mathrm{2}} −{Q}−\alpha^{\mathrm{4}} }\:+\frac{{P}^{\mathrm{2}} −{Q}}{\mathrm{2}}{sin}^{−\mathrm{1}} \left(\frac{\alpha^{\mathrm{2}} }{\:\sqrt{{P}^{\mathrm{2}} −{Q}}}\right)\right. \\ $$$${pls}\:{check}\:{upto}\:{this}\:…{nxt}\:{step}\:{put}\:{P}\:{and}\:{Q} \\ $$$${maximize}\:{area} \\ $$$${then}\:{finally}\:{R} \\ $$
Answered by ajfour last updated on 18/Jul/19
![let circle eq. be x^2 +(y−c)^2 =r^2 Also let r𝛉=(s/2) Intersection of parabola and circle on the right be P (h,h^2 ). h^2 =c+rcos θ , h=rsin θ (A/2)=∫_0 ^( h^2 ) (√y)dy−((r^2 sin θcos θ)/2)+((r^2 θ)/2) A = ((4h^3 )/3)−r^2 sin θcos θ+r^2 θ A=((s/(2θ)))^2 [((2s)/(3θ))sin^3 θ−sin θcos θ+θ] (dA/dθ)=−(s^2 /(2θ^3 ))[((2s)/(3θ))sin^3 θ−sin θcos θ+θ] +(s^2 /(4θ^2 ))[−((2s)/(3θ^3 ))sin^3 θ+((2s)/θ)sin^2 θ−cos^2 θ +sin^2 θ+1] ⇒ ((4s)/(3θ))sin^3 θ−2sin θcos θ+2θ = −((2s)/(3θ^2 ))+2ssin^2 θ−θcos^2 θ+θsin^2 θ+θ .....](https://www.tinkutara.com/question/Q64473.png)
$${let}\:{circle}\:{eq}.\:{be}\:\:\boldsymbol{{x}}^{\mathrm{2}} +\left(\boldsymbol{{y}}−\boldsymbol{{c}}\right)^{\mathrm{2}} =\boldsymbol{{r}}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:{Also}\:\:{let}\:\:\:\:\boldsymbol{{r}\theta}=\frac{\boldsymbol{{s}}}{\mathrm{2}} \\ $$$${Intersection}\:{of}\:{parabola}\:{and} \\ $$$${circle}\:{on}\:{the}\:{right}\:{be}\:\boldsymbol{{P}}\:\left(\boldsymbol{{h}},\boldsymbol{{h}}^{\mathrm{2}} \right). \\ $$$$\:\:\:\:{h}^{\mathrm{2}} ={c}+{r}\mathrm{cos}\:\theta\:\:,\:\:{h}={r}\mathrm{sin}\:\theta \\ $$$$\frac{\boldsymbol{{A}}}{\mathrm{2}}=\int_{\mathrm{0}} ^{\:\:{h}^{\mathrm{2}} } \sqrt{{y}}{dy}−\frac{{r}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta}{\mathrm{2}}+\frac{{r}^{\mathrm{2}} \theta}{\mathrm{2}} \\ $$$$\:\:\:\:\:{A}\:=\:\frac{\mathrm{4}{h}^{\mathrm{3}} }{\mathrm{3}}−{r}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta+{r}^{\mathrm{2}} \theta \\ $$$$\:\:{A}=\left(\frac{{s}}{\mathrm{2}\theta}\right)^{\mathrm{2}} \left[\frac{\mathrm{2}{s}}{\mathrm{3}\theta}\mathrm{sin}\:^{\mathrm{3}} \theta−\mathrm{sin}\:\theta\mathrm{cos}\:\theta+\theta\right] \\ $$$$\frac{{dA}}{{d}\theta}=−\frac{{s}^{\mathrm{2}} }{\mathrm{2}\theta^{\mathrm{3}} }\left[\frac{\mathrm{2}{s}}{\mathrm{3}\theta}\mathrm{sin}\:^{\mathrm{3}} \theta−\mathrm{sin}\:\theta\mathrm{cos}\:\theta+\theta\right] \\ $$$$\:\:+\frac{{s}^{\mathrm{2}} }{\mathrm{4}\theta^{\mathrm{2}} }\left[−\frac{\mathrm{2}{s}}{\mathrm{3}\theta^{\mathrm{3}} }\mathrm{sin}\:^{\mathrm{3}} \theta+\frac{\mathrm{2}{s}}{\theta}\mathrm{sin}\:^{\mathrm{2}} \theta−\mathrm{cos}\:^{\mathrm{2}} \theta\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{1}\right] \\ $$$$\Rightarrow\:\:\frac{\mathrm{4}{s}}{\mathrm{3}\theta}\mathrm{sin}\:^{\mathrm{3}} \theta−\mathrm{2sin}\:\theta\mathrm{cos}\:\theta+\mathrm{2}\theta \\ $$$$=\:−\frac{\mathrm{2}{s}}{\mathrm{3}\theta^{\mathrm{2}} }+\mathrm{2}{s}\mathrm{sin}\:^{\mathrm{2}} \theta−\theta\mathrm{cos}\:^{\mathrm{2}} \theta+\theta\mathrm{sin}\:^{\mathrm{2}} \theta+\theta \\ $$$$….. \\ $$
Commented by ajfour last updated on 18/Jul/19
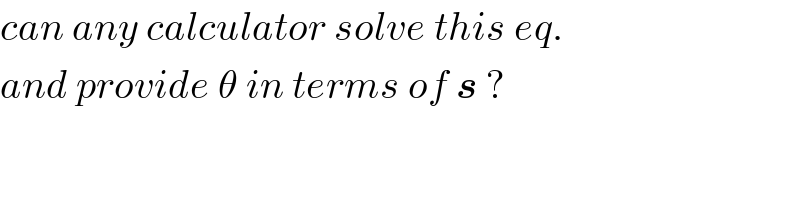
$${can}\:{any}\:{calculator}\:{solve}\:{this}\:{eq}. \\ $$$${and}\:{provide}\:\theta\:{in}\:{terms}\:{of}\:\boldsymbol{{s}}\:? \\ $$
