Question Number 130082 by benjo_mathlover last updated on 22/Jan/21
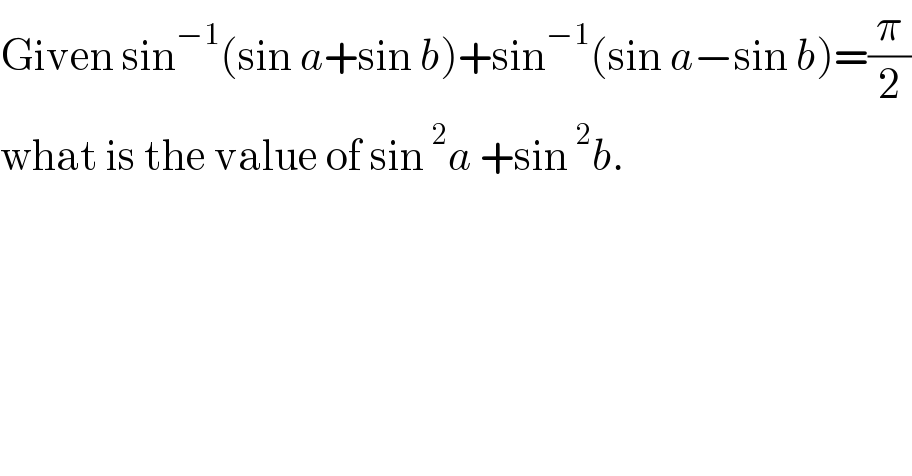
$$\mathrm{Given}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{a}+\mathrm{sin}\:{b}\right)+\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{a}−\mathrm{sin}\:{b}\right)=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{sin}\:^{\mathrm{2}} {a}\:+\mathrm{sin}\:^{\mathrm{2}} {b}. \\ $$
Answered by liberty last updated on 22/Jan/21

$$\:\mathrm{let}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{a}+\mathrm{sin}\:{b}\right)={p} \\ $$$$\:\Leftrightarrow\:\mathrm{sin}\:{a}\:+\:\mathrm{sin}\:{b}\:=\:\mathrm{sin}\:{p} \\ $$$$\:\mathrm{let}\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{sin}\:{a}−\mathrm{sin}\:{b}\right)={q} \\ $$$$\Leftrightarrow\:\mathrm{sin}\:{a}−\mathrm{sin}\:{b}\:=\:\mathrm{sin}\:{q} \\ $$$$\mathrm{and}\:{p}+{q}\:=\:\frac{\pi}{\mathrm{2}};\:{p}=\frac{\pi}{\mathrm{2}}−{q} \\ $$$$\Rightarrow\:\mathrm{sin}\:{p}\:=\:\mathrm{cos}\:{q}\: \\ $$$$\Rightarrow\mathrm{sin}\:^{\mathrm{2}} {p}\:=\:\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {q}\:{or}\:\mathrm{sin}\:^{\mathrm{2}} {p}+\mathrm{sin}\:^{\mathrm{2}} {q}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{sin}\:^{\mathrm{2}} {a}+\mathrm{2sin}\:{a}\:\mathrm{sin}\:{b}+\mathrm{sin}\:^{\mathrm{2}} {b}\:=\mathrm{sin}\:^{\mathrm{2}} {p}…\left(\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{sin}\:^{\mathrm{2}} {a}−\mathrm{2sin}\:{a}\:\mathrm{sin}\:{b}+\mathrm{sin}\:^{\mathrm{2}} {b}=\mathrm{sin}\:^{\mathrm{2}} {q}…\left(\mathrm{2}\right) \\ $$$${adding}\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right){give} \\ $$$$\:\mathrm{2}\left(\mathrm{sin}\:^{\mathrm{2}} {a}+\mathrm{sin}\:^{\mathrm{2}} {b}\right)=\:\mathrm{1}\: \\ $$$${then}\:{we}\:{get}\:\mathrm{sin}\:^{\mathrm{2}} {a}+\mathrm{sin}\:^{\mathrm{2}} {b}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
