Question Number 130508 by Raxreedoroid last updated on 26/Jan/21
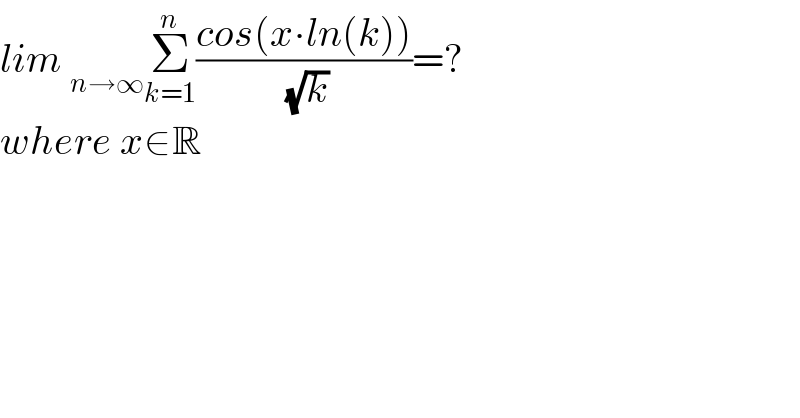
$${lim}\:_{{n}\rightarrow\infty} \underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{cos}\left({x}\centerdot{ln}\left({k}\right)\right)}{\:\sqrt{{k}}}=? \\ $$$${where}\:{x}\in\mathbb{R} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Jan/21
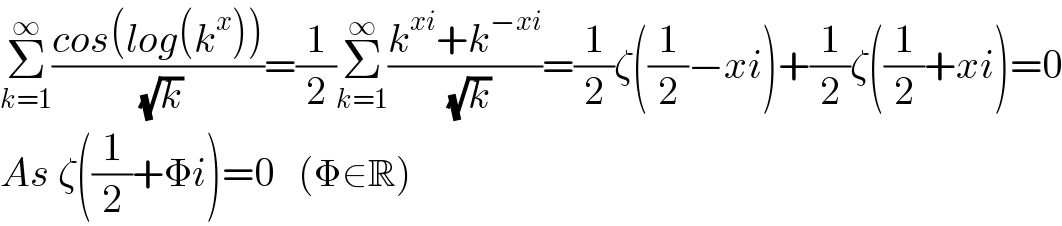
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{cos}\left({log}\left({k}^{{x}} \right)\right)}{\:\sqrt{{k}}}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{k}^{{xi}} +{k}^{−{xi}} }{\:\sqrt{{k}}}=\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}−{xi}\right)+\frac{\mathrm{1}}{\mathrm{2}}\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}+{xi}\right)=\mathrm{0} \\ $$$${As}\:\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}+\Phi{i}\right)=\mathrm{0}\:\:\:\left(\Phi\in\mathbb{R}\right) \\ $$
Commented by Raxreedoroid last updated on 26/Jan/21
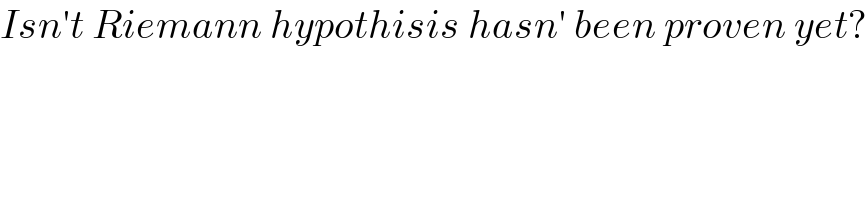
$${Isn}'{t}\:{Riemann}\:{hypothisis}\:{hasn}'\:{been}\:{proven}\:{yet}? \\ $$
