Menu Close

find-0-1-arctan-x-2-x-1-dx-

Tinku Tara 0 Comments
Pin




Question Number 130531 by mathmax by abdo last updated on 26/Jan/21
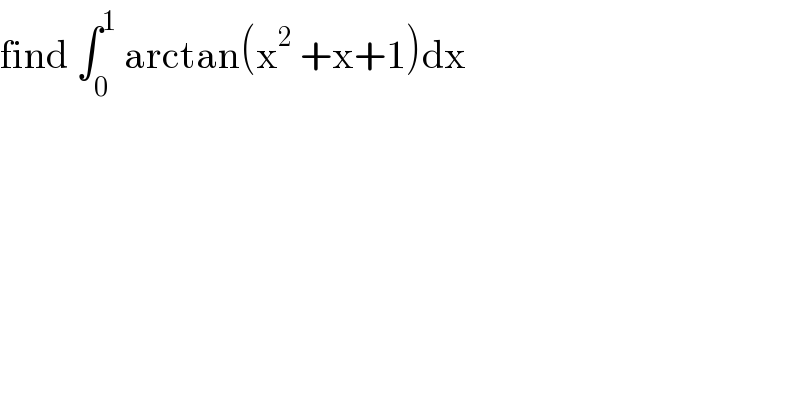
find ∫_0 ^1 arctan(x^2 +x+1)dx
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{arctan}\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)\mathrm{dx} \\ $$
Answered by Lordose last updated on 26/Jan/21
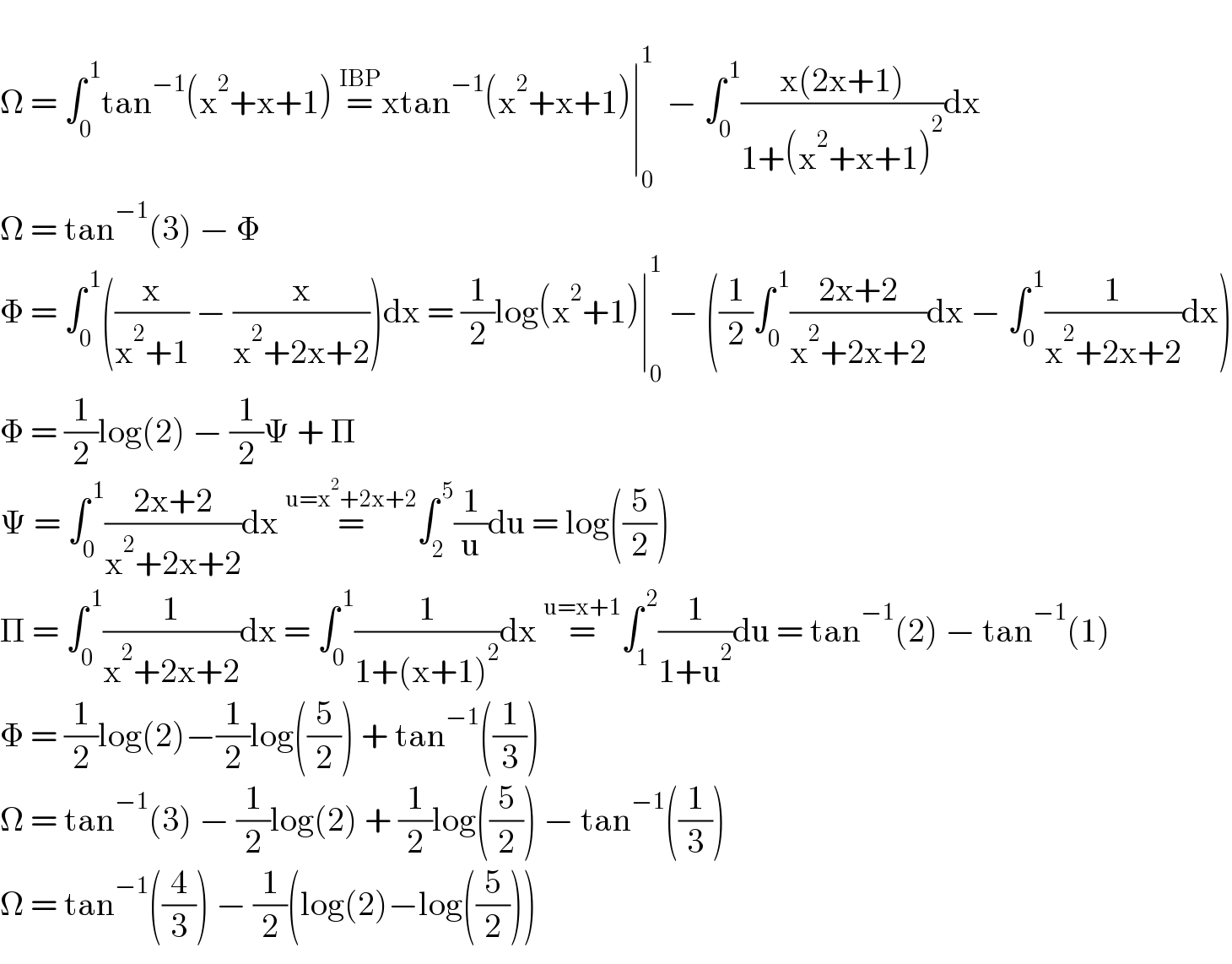
Ω = ∫_0 ^( 1) tan^(−1) (x^2 +x+1) =^(IBP) xtan^(−1) (x^2 +x+1)∣_0 ^1 − ∫_0 ^( 1) ((x(2x+1))/(1+(x^2 +x+1)^2 ))dx Ω = tan^(−1) (3) − Φ Φ = ∫_0 ^( 1) ((x/(x^2 +1)) − (x/(x^2 +2x+2)))dx = (1/2)log(x^2 +1)∣_0 ^1 − ((1/2)∫_0 ^( 1) ((2x+2)/(x^2 +2x+2))dx − ∫_0 ^( 1) (1/(x^2 +2x+2))dx) Φ = (1/2)log(2) − (1/2)Ψ + Π Ψ = ∫_0 ^( 1) ((2x+2)/(x^2 +2x+2))dx =^(u=x^2 +2x+2) ∫_2 ^( 5) (1/u)du = log((5/2)) Π = ∫_0 ^( 1) (1/(x^2 +2x+2))dx = ∫_0 ^( 1) (1/(1+(x+1)^2 ))dx =^(u=x+1) ∫_1 ^( 2) (1/(1+u^2 ))du = tan^(−1) (2) − tan^(−1) (1) Φ = (1/2)log(2)−(1/2)log((5/2)) + tan^(−1) ((1/3)) Ω = tan^(−1) (3) − (1/2)log(2) + (1/2)log((5/2)) − tan^(−1) ((1/3)) Ω = tan^(−1) ((4/3)) − (1/2)(log(2)−log((5/2)))
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\:\overset{\mathrm{IBP}} {=}\mathrm{xtan}^{−\mathrm{1}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:\:−\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}\left(\mathrm{2x}+\mathrm{1}\right)}{\mathrm{1}+\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}\right)\:−\:\Phi \\ $$$$\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:−\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}\right)\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:−\:\left(\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}\mathrm{dx}\:−\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}\mathrm{dx}\right) \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2}\right)\:−\:\frac{\mathrm{1}}{\mathrm{2}}\Psi\:+\:\Pi \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2x}+\mathrm{2}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}} {=}\int_{\mathrm{2}} ^{\:\mathrm{5}} \frac{\mathrm{1}}{\mathrm{u}}\mathrm{du}\:=\:\mathrm{log}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\: \\ $$$$\Pi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{2}}\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\overset{\mathrm{u}=\mathrm{x}+\mathrm{1}} {=}\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}\right)\:−\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)\: \\ $$$$\Phi\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:+\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}\right)\:−\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\mathrm{2}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:−\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$\Omega\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:−\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{log}\left(\mathrm{2}\right)−\mathrm{log}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\right) \\ $$
Commented by mathmax by abdo last updated on 26/Jan/21
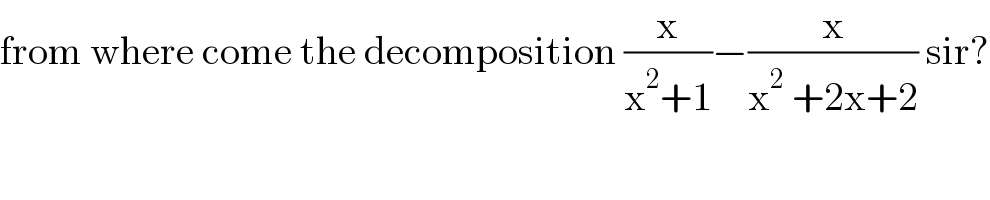
from where come the decomposition (x/(x^2 +1))−(x/(x^2 +2x+2)) sir?
$$\mathrm{from}\:\mathrm{where}\:\mathrm{come}\:\mathrm{the}\:\mathrm{decomposition}\:\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{2x}+\mathrm{2}}\:\mathrm{sir}? \\ $$
Commented by Lordose last updated on 27/Jan/21
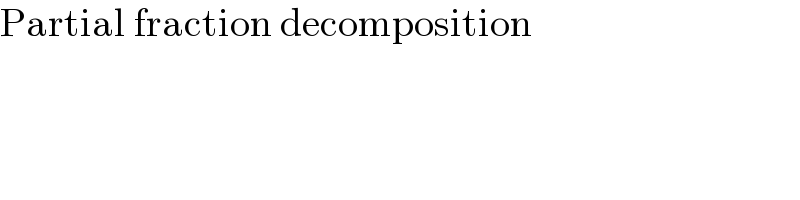
Partial fraction decomposition
$$\mathrm{Partial}\:\mathrm{fraction}\:\mathrm{decomposition} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *