Question Number 130530 by mathmax by abdo last updated on 26/Jan/21
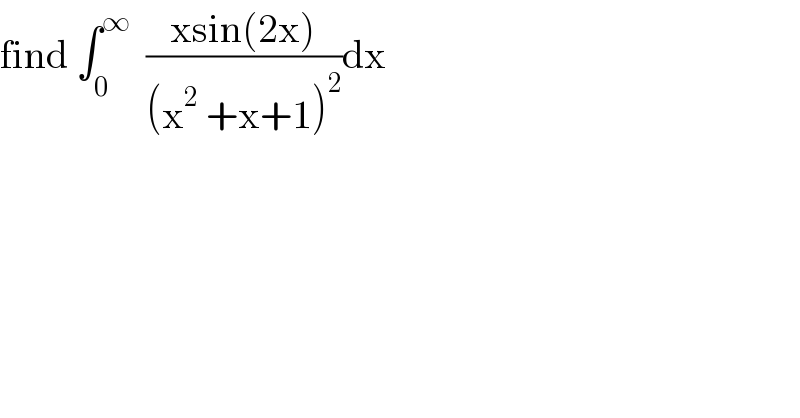
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{xsin}\left(\mathrm{2x}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 27/Jan/21
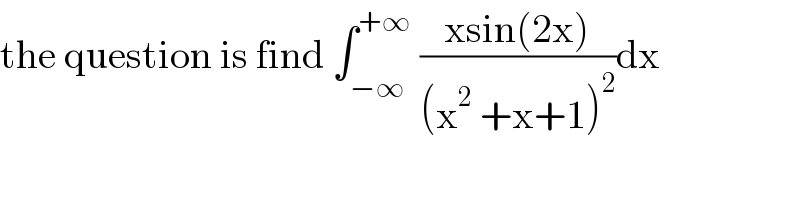
$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{find}\:\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xsin}\left(\mathrm{2x}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 28/Jan/21

$$\mathrm{A}=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xsin}\left(\mathrm{2x}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\mathrm{A}\:=\mathrm{Im}\left(\int_{−\infty} ^{+\infty} \:\frac{\mathrm{xe}^{\mathrm{2ix}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right)\mathrm{let} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{ze}^{\mathrm{2iz}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{2}} \:+\mathrm{z}+\mathrm{1}\:=\mathrm{0}\rightarrow\Delta=−\mathrm{3}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} =\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{ze}^{\mathrm{2iz}} }{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} }\:\mathrm{so}\:\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\varphi\:\mathrm{are}\:\mathrm{z}_{\mathrm{i}} \left(\mathrm{doubles}\right) \\ $$$$\mathrm{and}\:\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right) \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} } \:\:\left\{\frac{\mathrm{ze}^{\mathrm{2iz}} }{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} } \:\:\:\:\frac{\left(\mathrm{e}^{\mathrm{2iz}} \:+\mathrm{2iz}\:\mathrm{e}^{\mathrm{2iz}} \right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} −\mathrm{2ze}^{\mathrm{2iz}} \left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)}{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} } \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} } \:\:\:\frac{\mathrm{e}^{\mathrm{2iz}} \left(\mathrm{1}+\mathrm{2iz}\right)\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)−\mathrm{2ze}^{\mathrm{2iz}} }{\left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{e}^{\mathrm{2ie}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} } \left\{\left(\mathrm{1}+\mathrm{2ie}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right)\left(\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)−\mathrm{2e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \right\}\right.}{\left(\mathrm{2isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{e}^{\mathrm{2i}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)} \left\{\left(\mathrm{1}+\mathrm{2i}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\left(\mathrm{i}\sqrt{\mathrm{3}}\right)−\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\right\}\right.}{\left(\mathrm{i}\sqrt{\mathrm{3}}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{e}^{−\sqrt{\mathrm{3}}} \mathrm{e}^{−\mathrm{i}} \left\{\left(\mathrm{1}−\mathrm{i}−\sqrt{\mathrm{3}}\right)\mathrm{i}\sqrt{\mathrm{3}}+\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}\right)}{−\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$$=\frac{\mathrm{e}^{−\sqrt{\mathrm{3}}} \:\mathrm{e}^{−\mathrm{i}} \left\{\mathrm{i}\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}}−\mathrm{3i}+\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}\right\}}{−\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$$=\frac{\mathrm{e}^{−\sqrt{\mathrm{3}}} \left(\mathrm{cos1}−\mathrm{isin1}\right)\left(\mathrm{1}+\sqrt{\mathrm{3}}−\mathrm{3i}\right)}{−\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}} \\ $$$$=\frac{\mathrm{e}^{−\sqrt{\mathrm{3}}} \left\{\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{cos}\left(\mathrm{1}\right)−\mathrm{3icos}\left(\mathrm{1}\right)−\mathrm{i}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{1}\right)−\mathrm{3sin}\left(\mathrm{1}\right)\right.}{−\mathrm{3}\sqrt{\mathrm{3}}\mathrm{i}}\:\Rightarrow \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi×\left(…\right) \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left\{….\right\}\:\Rightarrow\mathrm{A}\:=−\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left(−\mathrm{3cos}\left(\mathrm{1}\right)−\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}\sqrt{\mathrm{3}}}\left(\mathrm{3cos}\left(\mathrm{1}\right)+\left(\mathrm{1}+\sqrt{\mathrm{3}}\right)\mathrm{sin}\left(\mathrm{1}\right)\right) \\ $$
