Question Number 513 by 112358 last updated on 25/Jan/15

$${What}\:{is}\:{the}\:{greatest}\:{common} \\ $$$${divisor}\:{of}\:{the}\:\mathrm{2010}\:{digit}\:{and}\:\mathrm{2005}\:{digit} \\ $$$${numbers}\:{below}? \\ $$$$\mathrm{222}…\mathrm{222}\:\left(\mathrm{2010}\:{of}\:{twos}\right) \\ $$$$\mathrm{777}…\mathrm{777}\:\left(\mathrm{2005}\:{of}\:{sevens}\right) \\ $$
Answered by prakash jain last updated on 22/Jan/15
![number1=2×(10^(2009) +10^(2008) +..+1) =((2×(10^(2010) −1))/9)=((2×[(10^5 )^(402) −1])/9) number2=((7×[(10^5 )^(401) −1])/9) gcd=((10^5 −1)/9)=((99999)/9)=11111](https://www.tinkutara.com/question/Q520.png)
$$\mathrm{number1}=\mathrm{2}×\left(\mathrm{10}^{\mathrm{2009}} +\mathrm{10}^{\mathrm{2008}} +..+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}×\left(\mathrm{10}^{\mathrm{2010}} −\mathrm{1}\right)}{\mathrm{9}}=\frac{\mathrm{2}×\left[\left(\mathrm{10}^{\mathrm{5}} \right)^{\mathrm{402}} −\mathrm{1}\right]}{\mathrm{9}} \\ $$$$\mathrm{number2}=\frac{\mathrm{7}×\left[\left(\mathrm{10}^{\mathrm{5}} \right)^{\mathrm{401}} −\mathrm{1}\right]}{\mathrm{9}} \\ $$$$\mathrm{gcd}=\frac{\mathrm{10}^{\mathrm{5}} −\mathrm{1}}{\mathrm{9}}=\frac{\mathrm{99999}}{\mathrm{9}}=\mathrm{11111} \\ $$
Commented by prakash jain last updated on 24/Jan/15
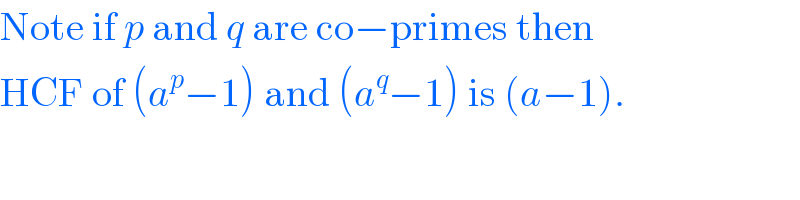
$$\mathrm{Note}\:\mathrm{if}\:{p}\:\mathrm{and}\:{q}\:\mathrm{are}\:\mathrm{co}−\mathrm{primes}\:\mathrm{then} \\ $$$$\mathrm{HCF}\:\mathrm{of}\:\left({a}^{{p}} −\mathrm{1}\right)\:\mathrm{and}\:\left({a}^{{q}} −\mathrm{1}\right)\:\mathrm{is}\:\left({a}−\mathrm{1}\right). \\ $$
