Question Number 65054 by behi83417@gmail.com last updated on 24/Jul/19
![{ (((√(x+y))+(√(x−y))=a)),((x^2 +y^2 =b [a,b∈R])) :}](https://www.tinkutara.com/question/Q65054.png)
$$\begin{cases}{\sqrt{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}}+\sqrt{\boldsymbol{\mathrm{x}}−\boldsymbol{\mathrm{y}}}=\boldsymbol{\mathrm{a}}}\\{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{y}}^{\mathrm{2}} =\boldsymbol{\mathrm{b}}\:\:\:\:\:\:\:\:\:\:\left[\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\in\boldsymbol{\mathrm{R}}\right]}\end{cases} \\ $$
Commented by behi83417@gmail.com last updated on 24/Jul/19
![thanks in advance proph. Abdo. [u+v=a⇒u^2 +v^2 +2uv=a^2 ]please check.](https://www.tinkutara.com/question/Q65072.png)
$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{proph}.\:\mathrm{Abdo}. \\ $$$$\left[\boldsymbol{\mathrm{u}}+\boldsymbol{\mathrm{v}}=\boldsymbol{\mathrm{a}}\Rightarrow\boldsymbol{\mathrm{u}}^{\mathrm{2}} +\boldsymbol{\mathrm{v}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{\mathrm{uv}}=\boldsymbol{\mathrm{a}}^{\mathrm{2}} \right]\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{check}}. \\ $$
Commented by mathmax by abdo last updated on 24/Jul/19

$${yes}\:{sir}\:… \\ $$
Answered by MJS last updated on 24/Jul/19
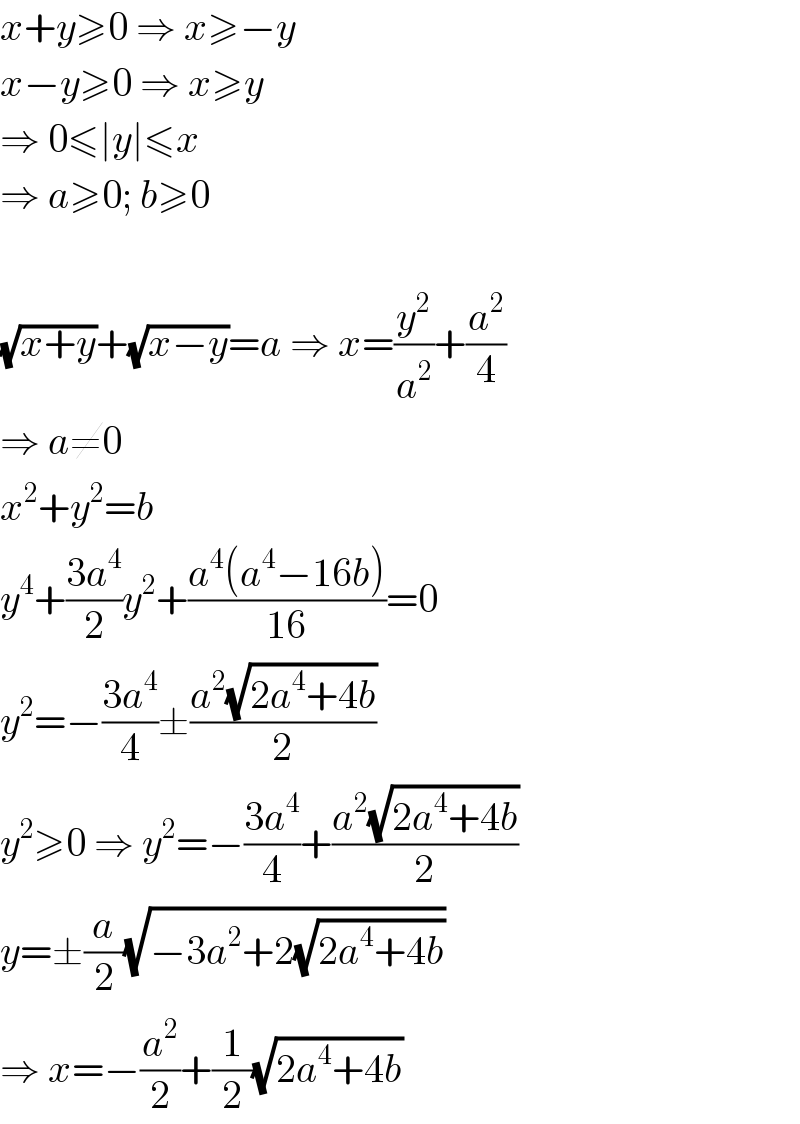
$${x}+{y}\geqslant\mathrm{0}\:\Rightarrow\:{x}\geqslant−{y} \\ $$$${x}−{y}\geqslant\mathrm{0}\:\Rightarrow\:{x}\geqslant{y} \\ $$$$\Rightarrow\:\mathrm{0}\leqslant\mid{y}\mid\leqslant{x} \\ $$$$\Rightarrow\:{a}\geqslant\mathrm{0};\:{b}\geqslant\mathrm{0} \\ $$$$ \\ $$$$\sqrt{{x}+{y}}+\sqrt{{x}−{y}}={a}\:\Rightarrow\:{x}=\frac{{y}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\:{a}\neq\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={b} \\ $$$${y}^{\mathrm{4}} +\frac{\mathrm{3}{a}^{\mathrm{4}} }{\mathrm{2}}{y}^{\mathrm{2}} +\frac{{a}^{\mathrm{4}} \left({a}^{\mathrm{4}} −\mathrm{16}{b}\right)}{\mathrm{16}}=\mathrm{0} \\ $$$${y}^{\mathrm{2}} =−\frac{\mathrm{3}{a}^{\mathrm{4}} }{\mathrm{4}}\pm\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}}}{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} \geqslant\mathrm{0}\:\Rightarrow\:{y}^{\mathrm{2}} =−\frac{\mathrm{3}{a}^{\mathrm{4}} }{\mathrm{4}}+\frac{{a}^{\mathrm{2}} \sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}}}{\mathrm{2}} \\ $$$${y}=\pm\frac{{a}}{\mathrm{2}}\sqrt{−\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}}} \\ $$$$\Rightarrow\:{x}=−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}} \\ $$
Commented by MJS last updated on 24/Jul/19
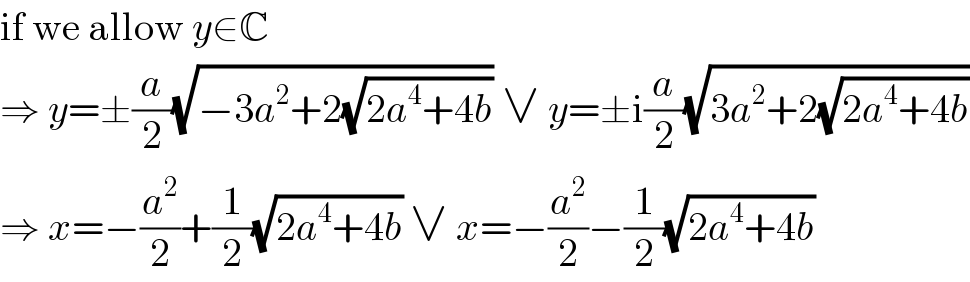
$$\mathrm{if}\:\mathrm{we}\:\mathrm{allow}\:{y}\in\mathbb{C} \\ $$$$\Rightarrow\:{y}=\pm\frac{{a}}{\mathrm{2}}\sqrt{−\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}}}\:\vee\:{y}=\pm\mathrm{i}\frac{{a}}{\mathrm{2}}\sqrt{\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}}} \\ $$$$\Rightarrow\:{x}=−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}}\:\vee\:{x}=−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}{a}^{\mathrm{4}} +\mathrm{4}{b}} \\ $$
Commented by MJS last updated on 24/Jul/19
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome},\:\mathrm{and}\:\mathrm{thank}\:\mathrm{you} \\ $$
Commented by behi83417@gmail.com last updated on 24/Jul/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{proph}:\mathrm{MJS}. \\ $$$$\mathrm{you}\:\mathrm{have}\:\mathrm{a}\:\mathrm{great}\:\mathrm{place}\:\mathrm{in}\:\mathrm{this}\:\mathrm{forum}\:\mathrm{and} \\ $$$$\mathrm{also}\:\mathrm{for}\:\mathrm{me}.\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 24/Jul/19
![x+y=p x−y=q ⇒(√p)+(√q)=a>0 (x+y)^2 +(x−y)^2 =2(x^2 +y^2 ) ⇒p^2 +q^2 =2b let P=(√p) ,Q=(√q) P+Q=a⇒Q=a−P P^4 +Q^4 =2b⇒P^4 +(a−P)^4 =2b ⇒2P^4 −4aP^3 +6a^2 P^2 −4a^3 P+a^4 −2b=0 let λ=(P/a) ⇒λ^4 −2λ^3 +3λ^2 −2λ+((1/2)−(b/a^4 ))=0 ⇒λ^4 −2λ^3 +3λ^2 −2λ+δ=0 ⇒λ_(1,2) =(1/2)[1±(√(4(√(1−δ))−3))] ⇒λ_(2,3) =(1/2)[1±i(√(4(√(1−δ))+3))] P_(1,2) =aλ=(a/2)[1±(√(4(√(1−δ))−3))] Q_(1,2) =a−(a/2)[1±(√(4(√(1−δ))−3))]=(a/2)[1∓(√(4(√(1−δ))−3))] P_(3,4) =aλ=(a/2)[1±i(√(4(√(1−δ))+3))] Q_(3,4) =a−(a/2)[1±i(√(4(√(1−δ))+3))]=(a/2)[1∓i(√(4(√(1−δ))+3))] x=((p+q)/2)=((P^2 +Q^2 )/2) y=((p−q)/2)=((P^2 −Q^2 )/2) ⇒x_(1,2) =(a^2 /8){[1±(√(4(√(1−δ))−3))]^2 +[1∓(√(4(√(1−δ))−3))]^2 } ⇒x_(1,2) =(1/2)a^2 (2(√(1−δ))−1) ⇒x_(1,2) =(1/2)[(√(2(a^4 +2b)))−a^2 ] ⇒x_(3,4) =(a^2 /8){[1±i(√(4(√(1−δ))+3))]^2 +[1∓i(√(4(√(1−δ))+3))]^2 } ⇒x_(3,4) =−(a^2 /2)(2(√(1−δ))+1) ⇒x_(3,4) =−(1/2)[(√(2(a^4 +2b)))+a^2 ] ⇒y_(1,2) =(a^2 /8){[1±(√(4(√(1−δ))−3))]^2 −[1∓(√(4(√(1−δ))−3))]^2 } ⇒y_(1,2) =±(a^2 /2)(√(4(√(1−δ))−3)) ⇒y_(1,2) =±(a/2)(√(2(√(2(a^4 +2b)))−3a^2 )) ⇒y_(3,4) =(a^2 /8){[1±i(√(4(√(1−δ))+3))]^2 −[1∓i(√(4(√(1−δ))+3))]^2 } ⇒y_(3,4) =±((a^2 i)/2)(√(4(√(1−δ))+3)) ⇒y_(3,4) =±((ai)/2)(√(2(√(2(a^4 +2b)))+3a^2 ))](https://www.tinkutara.com/question/Q65076.png)
$${x}+{y}={p} \\ $$$${x}−{y}={q} \\ $$$$\Rightarrow\sqrt{{p}}+\sqrt{{q}}={a}>\mathrm{0} \\ $$$$\left({x}+{y}\right)^{\mathrm{2}} +\left({x}−{y}\right)^{\mathrm{2}} =\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{q}^{\mathrm{2}} =\mathrm{2}{b} \\ $$$${let}\:{P}=\sqrt{{p}}\:,{Q}=\sqrt{{q}} \\ $$$${P}+{Q}={a}\Rightarrow{Q}={a}−{P} \\ $$$${P}^{\mathrm{4}} +{Q}^{\mathrm{4}} =\mathrm{2}{b}\Rightarrow{P}^{\mathrm{4}} +\left({a}−{P}\right)^{\mathrm{4}} =\mathrm{2}{b} \\ $$$$\Rightarrow\mathrm{2}{P}^{\mathrm{4}} −\mathrm{4}{aP}^{\mathrm{3}} +\mathrm{6}{a}^{\mathrm{2}} {P}^{\mathrm{2}} −\mathrm{4}{a}^{\mathrm{3}} {P}+{a}^{\mathrm{4}} −\mathrm{2}{b}=\mathrm{0} \\ $$$${let}\:\lambda=\frac{{P}}{{a}} \\ $$$$\Rightarrow\lambda^{\mathrm{4}} −\mathrm{2}\lambda^{\mathrm{3}} +\mathrm{3}\lambda^{\mathrm{2}} −\mathrm{2}\lambda+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{{b}}{{a}^{\mathrm{4}} }\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda^{\mathrm{4}} −\mathrm{2}\lambda^{\mathrm{3}} +\mathrm{3}\lambda^{\mathrm{2}} −\mathrm{2}\lambda+\delta=\mathrm{0} \\ $$$$\Rightarrow\lambda_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}\pm\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right] \\ $$$$\Rightarrow\lambda_{\mathrm{2},\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}\pm{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right] \\ $$$${P}_{\mathrm{1},\mathrm{2}} ={a}\lambda=\frac{{a}}{\mathrm{2}}\left[\mathrm{1}\pm\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right] \\ $$$${Q}_{\mathrm{1},\mathrm{2}} ={a}−\frac{{a}}{\mathrm{2}}\left[\mathrm{1}\pm\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right]=\frac{{a}}{\mathrm{2}}\left[\mathrm{1}\mp\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right] \\ $$$${P}_{\mathrm{3},\mathrm{4}} ={a}\lambda=\frac{{a}}{\mathrm{2}}\left[\mathrm{1}\pm{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right] \\ $$$${Q}_{\mathrm{3},\mathrm{4}} ={a}−\frac{{a}}{\mathrm{2}}\left[\mathrm{1}\pm{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right]=\frac{{a}}{\mathrm{2}}\left[\mathrm{1}\mp{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right] \\ $$$${x}=\frac{{p}+{q}}{\mathrm{2}}=\frac{{P}^{\mathrm{2}} +{Q}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${y}=\frac{{p}−{q}}{\mathrm{2}}=\frac{{P}^{\mathrm{2}} −{Q}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow{x}_{\mathrm{1},\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left\{\left[\mathrm{1}\pm\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right]^{\mathrm{2}} +\left[\mathrm{1}\mp\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right]^{\mathrm{2}} \right\} \\ $$$$\Rightarrow{x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{2}} \left(\mathrm{2}\sqrt{\mathrm{1}−\delta}−\mathrm{1}\right) \\ $$$$\Rightarrow{x}_{\mathrm{1},\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt{\mathrm{2}\left({a}^{\mathrm{4}} +\mathrm{2}{b}\right)}−{a}^{\mathrm{2}} \right] \\ $$$$\Rightarrow{x}_{\mathrm{3},\mathrm{4}} =\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left\{\left[\mathrm{1}\pm{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right]^{\mathrm{2}} +\left[\mathrm{1}\mp{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right]^{\mathrm{2}} \right\} \\ $$$$\Rightarrow{x}_{\mathrm{3},\mathrm{4}} =−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\sqrt{\mathrm{1}−\delta}+\mathrm{1}\right) \\ $$$$\Rightarrow{x}_{\mathrm{3},\mathrm{4}} =−\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt{\mathrm{2}\left({a}^{\mathrm{4}} +\mathrm{2}{b}\right)}+{a}^{\mathrm{2}} \right] \\ $$$$\Rightarrow{y}_{\mathrm{1},\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left\{\left[\mathrm{1}\pm\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right]^{\mathrm{2}} −\left[\mathrm{1}\mp\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}}\right]^{\mathrm{2}} \right\} \\ $$$$\Rightarrow{y}_{\mathrm{1},\mathrm{2}} =\pm\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}−\mathrm{3}} \\ $$$$\Rightarrow{y}_{\mathrm{1},\mathrm{2}} =\pm\frac{{a}}{\mathrm{2}}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\left({a}^{\mathrm{4}} +\mathrm{2}{b}\right)}−\mathrm{3}{a}^{\mathrm{2}} } \\ $$$$\Rightarrow{y}_{\mathrm{3},\mathrm{4}} =\frac{{a}^{\mathrm{2}} }{\mathrm{8}}\left\{\left[\mathrm{1}\pm{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right]^{\mathrm{2}} −\left[\mathrm{1}\mp{i}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}}\right]^{\mathrm{2}} \right\} \\ $$$$\Rightarrow{y}_{\mathrm{3},\mathrm{4}} =\pm\frac{{a}^{\mathrm{2}} {i}}{\mathrm{2}}\sqrt{\mathrm{4}\sqrt{\mathrm{1}−\delta}+\mathrm{3}} \\ $$$$\Rightarrow{y}_{\mathrm{3},\mathrm{4}} =\pm\frac{{ai}}{\mathrm{2}}\sqrt{\mathrm{2}\sqrt{\mathrm{2}\left({a}^{\mathrm{4}} +\mathrm{2}{b}\right)}+\mathrm{3}{a}^{\mathrm{2}} } \\ $$
Commented by behi83417@gmail.com last updated on 24/Jul/19

$$\mathrm{my}\:\mathrm{master}\:\mathrm{is}\:\mathrm{coming}! \\ $$$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{dear}\:\mathrm{master}. \\ $$$$\mathrm{your}\:\mathrm{answers}\:\mathrm{don}'\mathrm{t}\:\mathrm{match}\:\mathrm{with}\:\mathrm{sir}\:\mathrm{MJS}'\mathrm{s}. \\ $$$$\mathrm{where}\:\mathrm{is}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{sir}? \\ $$
Commented by mr W last updated on 25/Jul/19
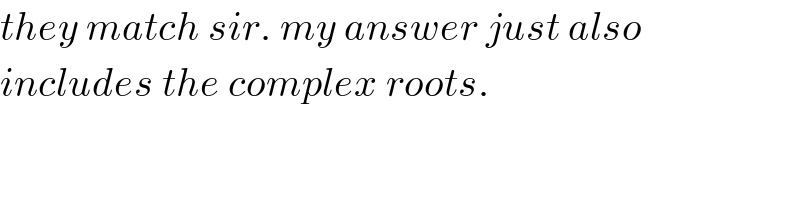
$${they}\:{match}\:{sir}.\:{my}\:{answer}\:{just}\:{also} \\ $$$${includes}\:{the}\:{complex}\:{roots}. \\ $$
