0-x-n-1-x-6-dx-

Question Number 130594 by Lordose last updated on 27/Jan/21

$$\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\mathrm{dx} \\ $$

Answered by mindispower last updated on 27/Jan/21

existe if n∈]−1,5[=∫_0 ^∞ (t^((n−5)/6) /(6(1+t)))dt=(1/6)∫_0 ^∞ (t^(((n+1)/6)−1) /((1+t)^(((n+1)/6)+((−n+5)/6) ) )) =(1/6)β(((n+1)/6),((5−n)/6))=(1/6).(π/(sin((((n+1)π)/6))))

$$\left.\:\:{existe}\:{if}\:{n}\in\right]−\mathrm{1},\mathrm{5}\left[=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{{n}−\mathrm{5}}{\mathrm{6}}} }{\mathrm{6}\left(\mathrm{1}+{t}\right)}{dt}=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{{n}+\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{\frac{{n}+\mathrm{1}}{\mathrm{6}}+\frac{−{n}+\mathrm{5}}{\mathrm{6}}\:} \:}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\beta\left(\frac{{n}+\mathrm{1}}{\mathrm{6}},\frac{\mathrm{5}−{n}}{\mathrm{6}}\right)=\frac{\mathrm{1}}{\mathrm{6}}.\frac{\pi}{{sin}\left(\frac{\left({n}+\mathrm{1}\right)\pi}{\mathrm{6}}\right)} \\ $$

Commented by Lordose last updated on 27/Jan/21

$$\mathrm{Gratitude} \\ $$

Answered by mathmax by abdo last updated on 27/Jan/21

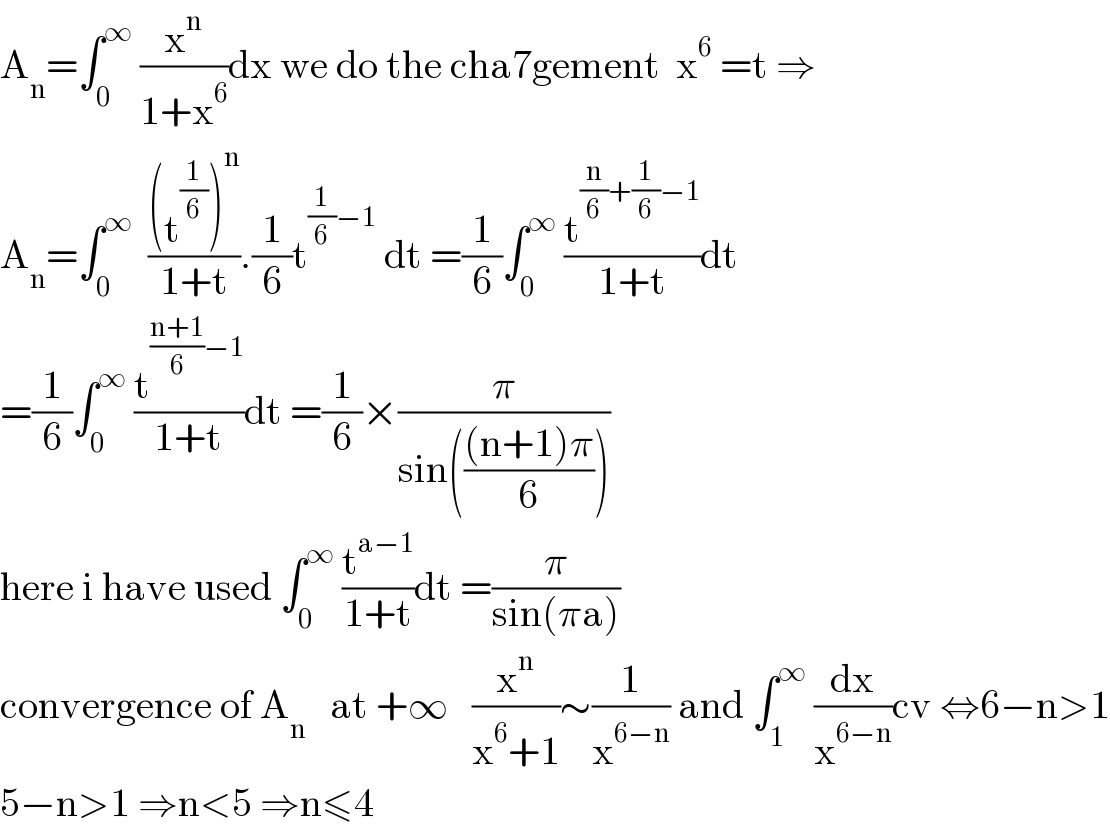
A_n =∫_0 ^∞ (x^n /(1+x^6 ))dx we do the cha7gement x^6 =t ⇒ A_n =∫_0 ^∞ (((t^(1/6) )^n )/(1+t)).(1/6)t^((1/6)−1) dt =(1/6)∫_0 ^∞ (t^((n/6)+(1/6)−1) /(1+t))dt =(1/6)∫_0 ^∞ (t^(((n+1)/6)−1) /(1+t))dt =(1/6)×(π/(sin((((n+1)π)/6)))) here i have used ∫_0 ^∞ (t^(a−1) /(1+t))dt =(π/(sin(πa))) convergence of A_n at +∞ (x^n /(x^6 +1))∼(1/x^(6−n) ) and ∫_1 ^∞ (dx/x^(6−n) )cv ⇔6−n>1 5−n>1 ⇒n<5 ⇒n≤4

$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{1}+\mathrm{x}^{\mathrm{6}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{cha7gement}\:\:\mathrm{x}^{\mathrm{6}} \:=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left(\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}} \right)^{\mathrm{n}} }{\mathrm{1}+\mathrm{t}}.\frac{\mathrm{1}}{\mathrm{6}}\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{n}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{n}+\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{6}}×\frac{\pi}{\mathrm{sin}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\pi}{\mathrm{6}}\right)} \\ $$$$\mathrm{here}\:\mathrm{i}\:\mathrm{have}\:\mathrm{used}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{a}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{a}\right)} \\ $$$$\mathrm{convergence}\:\mathrm{of}\:\mathrm{A}_{\mathrm{n}} \:\:\:\mathrm{at}\:+\infty\:\:\:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}\sim\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{6}−\mathrm{n}} }\:\mathrm{and}\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{6}−\mathrm{n}} }\mathrm{cv}\:\Leftrightarrow\mathrm{6}−\mathrm{n}>\mathrm{1} \\ $$$$\mathrm{5}−\mathrm{n}>\mathrm{1}\:\Rightarrow\mathrm{n}<\mathrm{5}\:\Rightarrow\mathrm{n}\leqslant\mathrm{4} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply