Menu Close

0-pi-cos-2-1-2acos-a-2-d-a-2-lt-1-answer-

Tinku Tara 0 Comments
Pin




Question Number 65202 by arcana last updated on 26/Jul/19
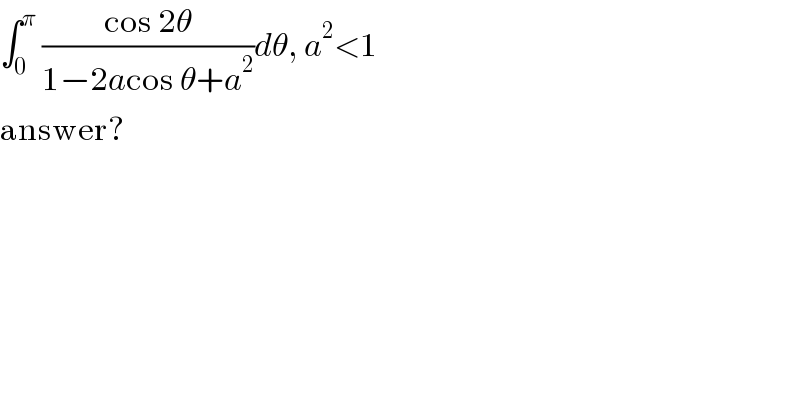
∫_0 ^π ((cos 2θ)/(1−2acos θ+a^2 ))dθ, a^2 <1 answer?
$$\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}−\mathrm{2}{a}\mathrm{cos}\:\theta+{a}^{\mathrm{2}} }{d}\theta,\:{a}^{\mathrm{2}} <\mathrm{1} \\ $$$$\mathrm{answer}? \\ $$
Answered by Tanmay chaudhury last updated on 26/Jul/19
formula taken from Sl loney ((1−a^2 )/(1−2acosθ+a^2 )) =1+2acosθ+2a^2 cos2θ+2a^3 cos3θ+... now I(r)=∫_0 ^π ((cosrθ)/(1−2acosθ+a^2 ))dθ =(1/(1−a^2 ))∫_0 ^π ((1−a^2 )/(1−2acosθ+a^2 ))×cosrθ dθ =(1/(1−a^2 ))∫_0 ^π (1+2acosθ+2a^2 cos2θ+2a^3 cos3θ+...)cosrθ dθ (1/(1−a^2 ))∫_0 ^π (cosrθ+2acosθcosrθ+..+2a^r cosrθ.cosrθ+...)dθ again formula ∫_0 ^π cosmθcosnθdθ=∫_0 ^π sinmθsinnθdθ=0 when m≠n if m=n then ∫_0 ^π cosmθcosnθdθ=(π/2) so I(r)=(1/(1−a^2 ))×(0+0+...+2a^r ×(π/2)) I(r)=((a^r π)/(1−a^2 )) so required answer=I(2)=((a^2 π)/(1−a^2 ))
$$\boldsymbol{{formula}}\:\boldsymbol{{taken}}\:\boldsymbol{{from}}\:\boldsymbol{{S}}{l}\:{loney} \\ $$$$\frac{\mathrm{1}−{a}^{\mathrm{2}} }{\mathrm{1}−\mathrm{2}{acos}\theta+{a}^{\mathrm{2}} } \\ $$$$=\mathrm{1}+\mathrm{2}{acos}\theta+\mathrm{2}{a}^{\mathrm{2}} {cos}\mathrm{2}\theta+\mathrm{2}{a}^{\mathrm{3}} {cos}\mathrm{3}\theta+… \\ $$$${now}\: \\ $$$${I}\left({r}\right)=\int_{\mathrm{0}} ^{\pi} \frac{{cosr}\theta}{\mathrm{1}−\mathrm{2}{acos}\theta+{a}^{\mathrm{2}} }{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}−{a}^{\mathrm{2}} }{\mathrm{1}−\mathrm{2}{acos}\theta+{a}^{\mathrm{2}} }×{cosr}\theta\:\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}+\mathrm{2}{acos}\theta+\mathrm{2}{a}^{\mathrm{2}} {cos}\mathrm{2}\theta+\mathrm{2}{a}^{\mathrm{3}} {cos}\mathrm{3}\theta+…\right){cosr}\theta\:{d}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \left({cosr}\theta+\mathrm{2}{acos}\theta{cosr}\theta+..+\mathrm{2}{a}^{{r}} {cosr}\theta.{cosr}\theta+…\right){d}\theta \\ $$$${again}\:{formula} \\ $$$$\int_{\mathrm{0}} ^{\pi} {cosm}\theta{cosn}\theta{d}\theta=\int_{\mathrm{0}} ^{\pi} {sinm}\theta{sinn}\theta{d}\theta=\mathrm{0} \\ $$$${when}\:{m}\neq{n} \\ $$$$\boldsymbol{{if}}\:\boldsymbol{{m}}=\boldsymbol{{n}}\:\:\:\boldsymbol{{then}}\:\int_{\mathrm{0}} ^{\pi} {cosm}\theta{cosn}\theta{d}\theta=\frac{\pi}{\mathrm{2}} \\ $$$${so}\: \\ $$$${I}\left({r}\right)=\frac{\mathrm{1}}{\mathrm{1}−{a}^{\mathrm{2}} }×\left(\mathrm{0}+\mathrm{0}+…+\mathrm{2}{a}^{{r}} ×\frac{\pi}{\mathrm{2}}\right) \\ $$$${I}\left({r}\right)=\frac{{a}^{{r}} \pi}{\mathrm{1}−{a}^{\mathrm{2}} } \\ $$$${so}\:{required}\:{answer}={I}\left(\mathrm{2}\right)=\frac{{a}^{\mathrm{2}} \pi}{\mathrm{1}−{a}^{\mathrm{2}} } \\ $$$$ \\ $$
Commented by arcana last updated on 26/Jul/19
gracias!
$$\mathrm{gracias}! \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *