Question Number 515 by 112358 last updated on 25/Jan/15
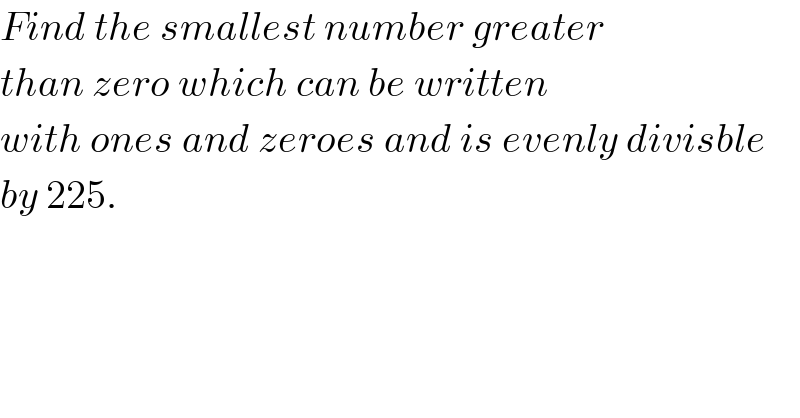
$${Find}\:{the}\:{smallest}\:{number}\:{greater} \\ $$$${than}\:{zero}\:{which}\:{can}\:{be}\:{written} \\ $$$${with}\:{ones}\:{and}\:{zeroes}\:{and}\:{is}\:{evenly}\:{divisble} \\ $$$${by}\:\mathrm{225}. \\ $$
Answered by prakash jain last updated on 22/Jan/15

$$\mathrm{225}=\mathrm{25}×\mathrm{9} \\ $$$$\mathrm{For}\:\mathrm{25},\:\mathrm{10}^{\mathrm{2}} \\ $$$$\mathrm{number}\:\mathrm{is}\:\mathrm{of}\:\mathrm{form}\:{n}\:=\underset{{i}=\mathrm{1}} {\overset{{j}} {\sum}}\mathrm{10}^{{k}_{{i}} } ,\:{k}_{{i}} \in\mathbb{N}\cup\left\{\mathrm{0}\right\} \\ $$$${n}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{9}.\: \\ $$$$\mathrm{Let}\:\mathrm{say}\:\mathrm{say}\:{k}_{{i}} >{k}_{{i}−\mathrm{1}} . \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{clear}\:\mathrm{that}\:\mathrm{for}\:\mathrm{smallest}\:{n}\:{k}_{\mathrm{1}} =\mathrm{0} \\ $$$$\frac{\mathrm{10}^{{k}_{{j}} } +\mathrm{10}^{{k}_{{j}−\mathrm{1}} } +\mathrm{10}^{{k}_{\mathrm{1}} } }{\mathrm{9}}=\frac{\left(\mathrm{10}^{{k}_{{j}} } −\mathrm{1}\right)+\left(\mathrm{10}^{{k}_{{j}−\mathrm{1}} } −\mathrm{1}\right)+…+\left(\mathrm{1}+{j}−\mathrm{1}\right)}{\mathrm{9}} \\ $$$$\mathrm{RHS}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{9}\:\mathrm{only}\:\mathrm{for}\:{j}=\mathrm{9} \\ $$$$\mathrm{So}\:\mathrm{9}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{needed}\:\mathrm{in}\:\mathrm{the}\:\mathrm{sum}. \\ $$$$\mathrm{For}\:\mathrm{smallest}\:\mathrm{value}\:\mathrm{for}\:{n} \\ $$$${n}=\underset{{k}=\mathrm{0}} {\overset{\mathrm{8}} {\sum}}\mathrm{10}^{{k}} =\mathrm{111111111} \\ $$$$\mathrm{Smallest}\:{n}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{form}\:\mathrm{for}\:\mathrm{225}. \\ $$$$\mathrm{11111111100} \\ $$
