Question Number 6439 by sanusihammed last updated on 27/Jun/16
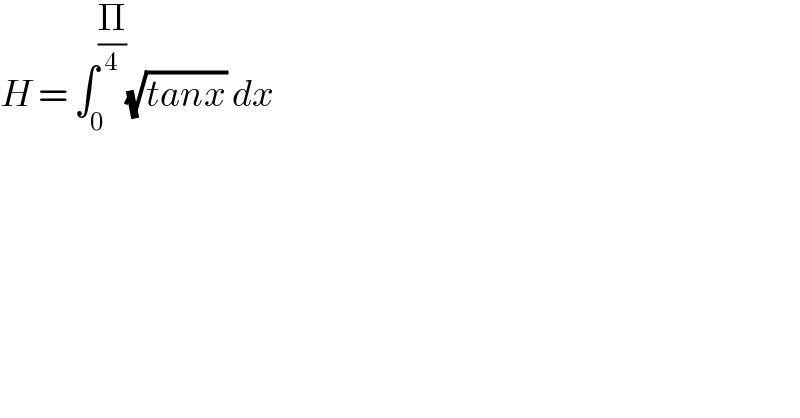
$${H}\:=\:\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{4}}} \sqrt{{tanx}}\:{dx}\: \\ $$
Commented by Temp last updated on 27/Jun/16
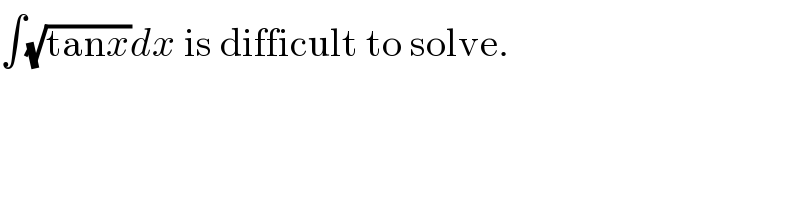
$$\int\sqrt{\mathrm{tan}{x}}{dx}\:\mathrm{is}\:\mathrm{difficult}\:\mathrm{to}\:\mathrm{solve}. \\ $$
Commented by nburiburu last updated on 27/Jun/16

$${by}\:{substitution}:\:{t}=\sqrt{{tan}\:{x}}\Rightarrow{t}^{\mathrm{2}} ={tan}\:{x} \\ $$$$\mathrm{2}{t}\:{dt}\:=\:{sec}^{\mathrm{2}} {x}\:{dx}\:=\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:{dx} \\ $$$${dx}=\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt} \\ $$$$\int{t}.\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt}=\int\frac{\mathrm{2}{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{4}} }\:{dt} \\ $$$${and}\:{from}\:{here}\:{it}\:{is}\:{rare}\:{but}\:{simplier}\:{with}\:{complex}\:{roots}\:{in}\:{a}\:{rational}\:{descomposition}. \\ $$
Commented by prakash jain last updated on 27/Jun/16
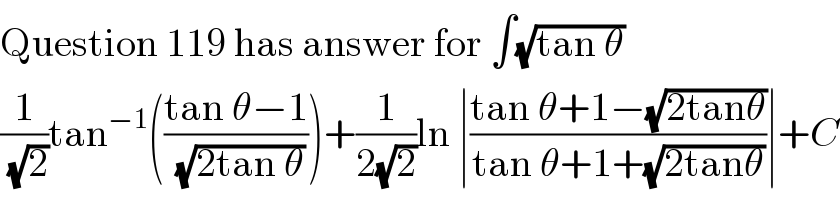
$$\mathrm{Question}\:\mathrm{119}\:\mathrm{has}\:\mathrm{answer}\:\mathrm{for}\:\int\sqrt{\mathrm{tan}\:\theta} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{tan}\:\theta−\mathrm{1}}{\:\sqrt{\mathrm{2tan}\:\theta}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\mid\frac{\mathrm{tan}\:\theta+\mathrm{1}−\sqrt{\mathrm{2tan}\theta}}{\mathrm{tan}\:\theta+\mathrm{1}+\sqrt{\mathrm{2tan}\theta}}\mid+{C} \\ $$
