Question Number 137528 by I want to learn more last updated on 03/Apr/21
Commented by I want to learn more last updated on 03/Apr/21
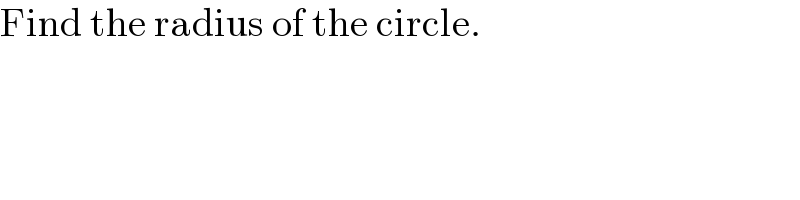
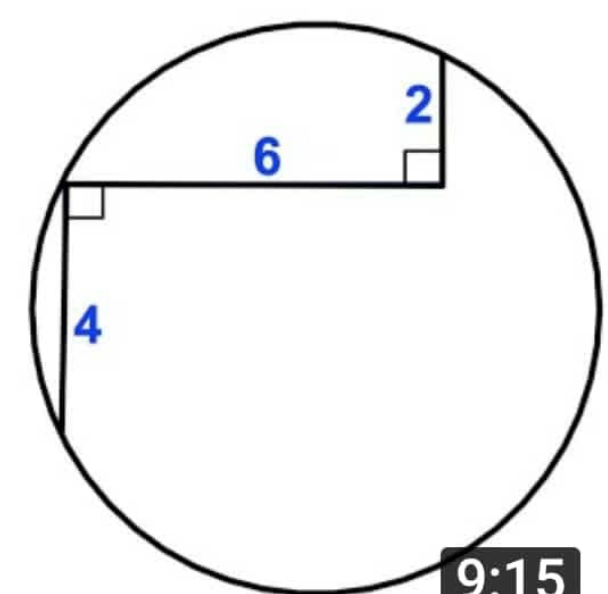
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circle}. \\ $$
Answered by mr W last updated on 03/Apr/21
Commented by mr W last updated on 03/Apr/21
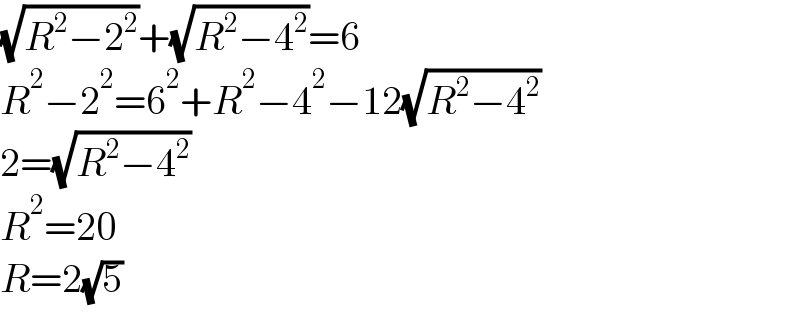
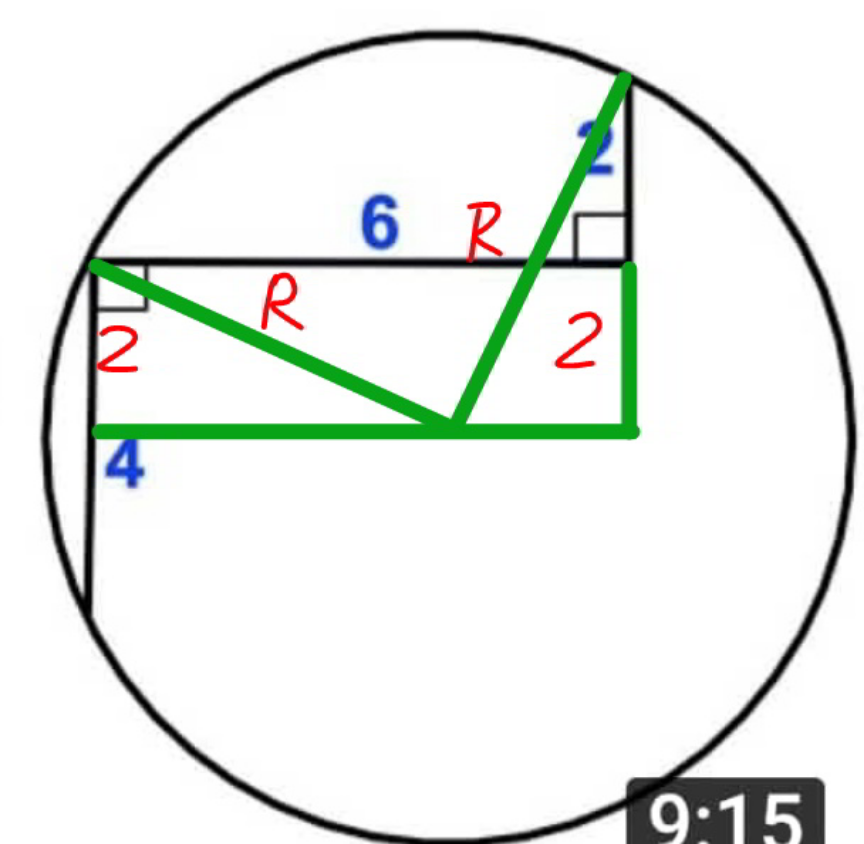
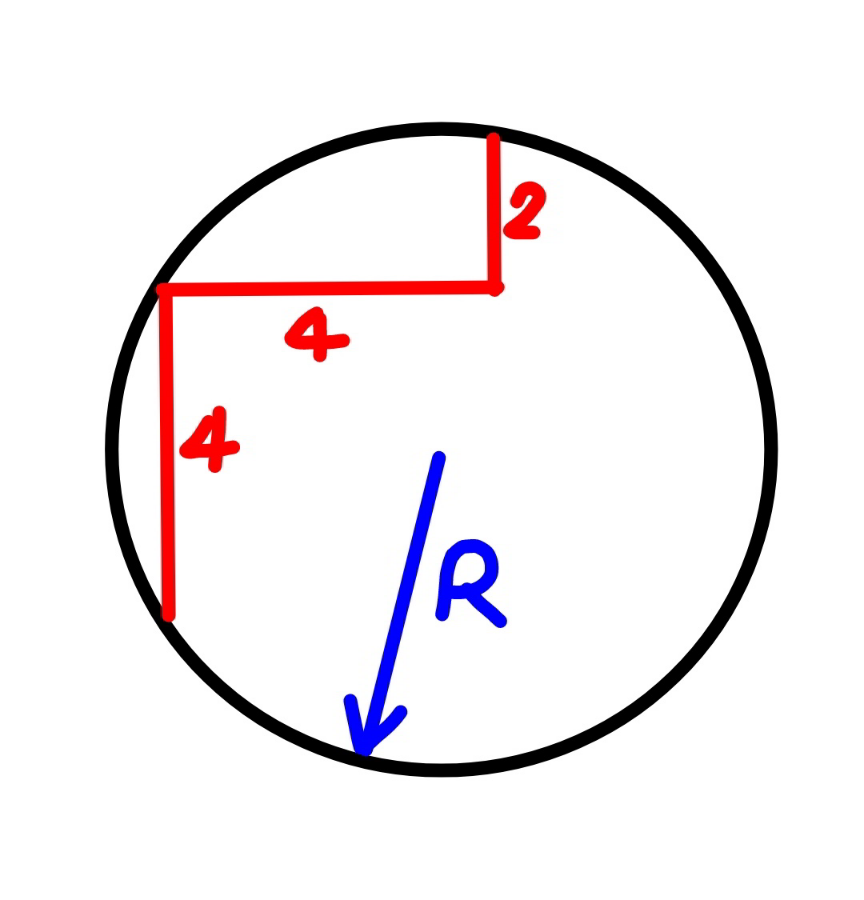
$$\sqrt{{R}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} }+\sqrt{{R}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} }=\mathrm{6} \\ $$$${R}^{\mathrm{2}} −\mathrm{2}^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} −\mathrm{12}\sqrt{{R}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} } \\ $$$$\mathrm{2}=\sqrt{{R}^{\mathrm{2}} −\mathrm{4}^{\mathrm{2}} } \\ $$$${R}^{\mathrm{2}} =\mathrm{20} \\ $$$${R}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$
Commented by I want to learn more last updated on 03/Apr/21
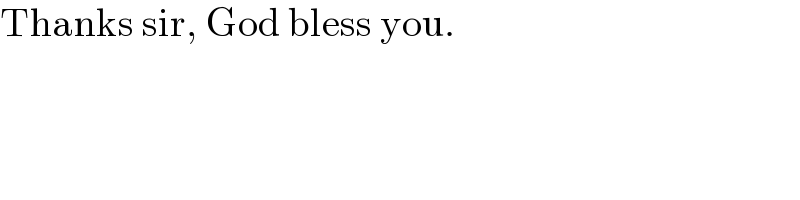
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Answered by mr W last updated on 03/Apr/21
Commented by mr W last updated on 03/Apr/21
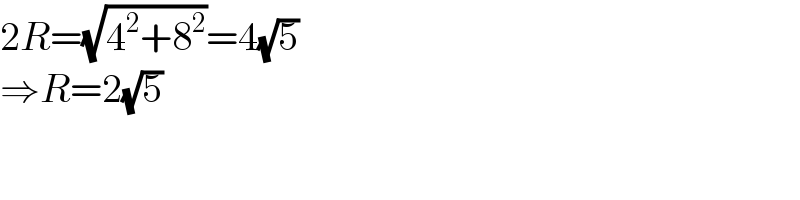
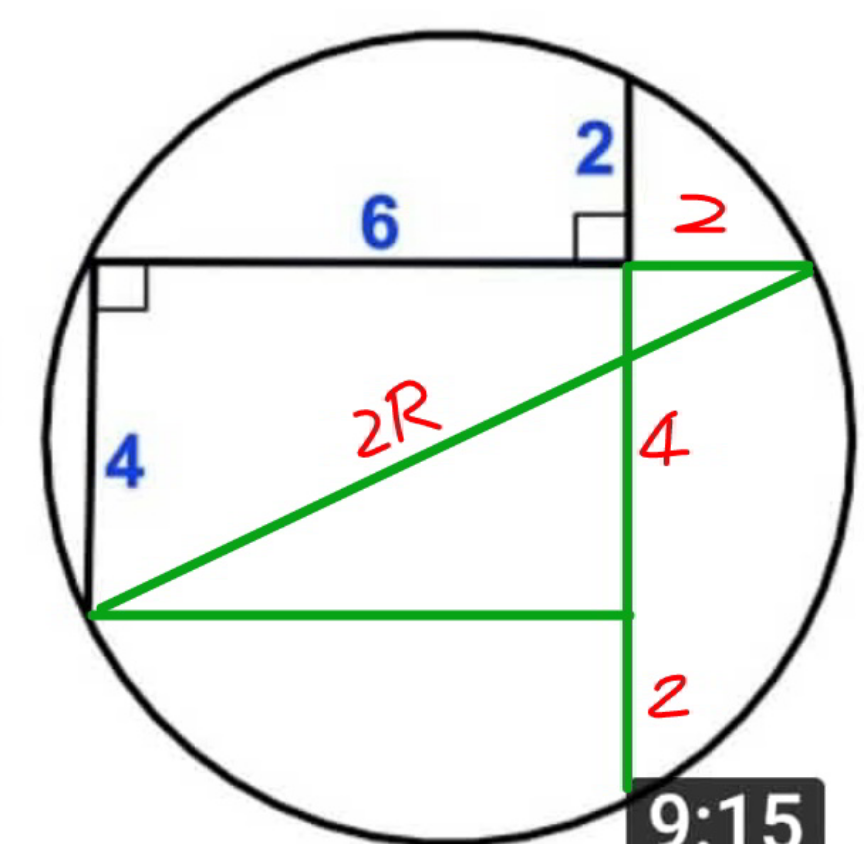
$$\mathrm{2}{R}=\sqrt{\mathrm{4}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{R}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$
Commented by I want to learn more last updated on 03/Apr/21
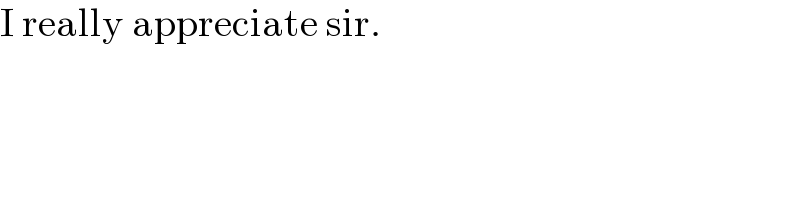
$$\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 03/Apr/21
$$\mathrm{Sir},\:\mathrm{most}\:\mathrm{people}\:\mathrm{got}\:\mathrm{radius}\:\:=\:\:\mathrm{5}. \\ $$
Commented by I want to learn more last updated on 03/Apr/21

$$\mathrm{But}\:\mathrm{i}\:\mathrm{understand}\:\mathrm{your}\:\mathrm{workings}\:\mathrm{sir}.\:\mathrm{They}\:\mathrm{are}\:\mathrm{judt}\:\mathrm{getting}\:\:\mathrm{5}. \\ $$
Commented by mr W last updated on 03/Apr/21

$${if}\:{you}\:{really}\:{have}\:{understood},\:{you} \\ $$$${should}\:{be}\:{able}\:{to}\:{know}\:{by}\:{yourself} \\ $$$${what}\:{is}\:{right}. \\ $$
Commented by I want to learn more last updated on 04/Apr/21

$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{know}. \\ $$
Answered by mr W last updated on 03/Apr/21
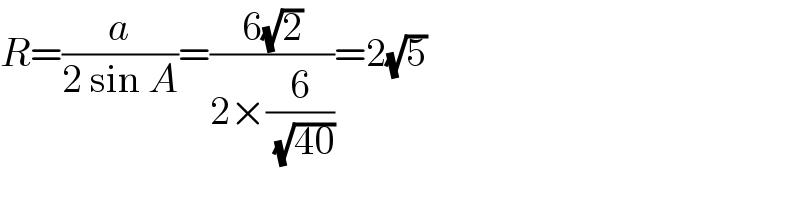
$${R}=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:{A}}=\frac{\mathrm{6}\sqrt{\mathrm{2}}}{\mathrm{2}×\frac{\mathrm{6}}{\:\sqrt{\mathrm{40}}}}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$
Commented by mr W last updated on 04/Apr/21
Commented by I want to learn more last updated on 04/Apr/21
$$\mathrm{Thanks}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
Commented by mr W last updated on 04/Apr/21

$${can}\:{you}\:{solve}\:{following}\:{case}\:{using} \\ $$$${this}\:{method}: \\ $$
Commented by mr W last updated on 05/Apr/21
Commented by mr W last updated on 05/Apr/21
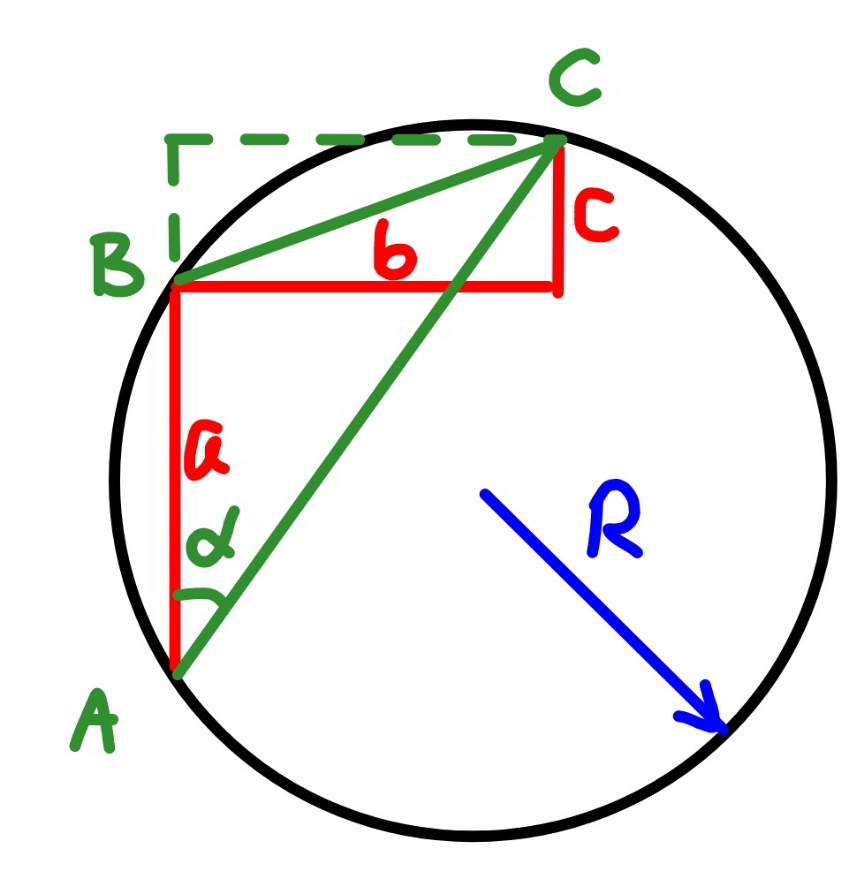
![BC=(√(b^2 +c^2 )) AC=(√(b^2 +(a+c)^2 )) sin α=(b/(AC))=(b/( (√(b^2 +(a+c)^2 )))) BC=2R sin α ⇒R=((√((b^2 +c^2 )[b^2 +(a+c)^2 ]))/(2b))](https://www.tinkutara.com/question/Q137670.png)
$${BC}=\sqrt{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$${AC}=\sqrt{{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:\alpha=\frac{{b}}{{AC}}=\frac{{b}}{\:\sqrt{{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} }} \\ $$$${BC}=\mathrm{2}{R}\:\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{R}=\frac{\sqrt{\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\left[{b}^{\mathrm{2}} +\left({a}+{c}\right)^{\mathrm{2}} \right]}}{\mathrm{2}{b}} \\ $$
Commented by I want to learn more last updated on 04/Apr/21

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}. \\ $$
Commented by mr W last updated on 05/Apr/21
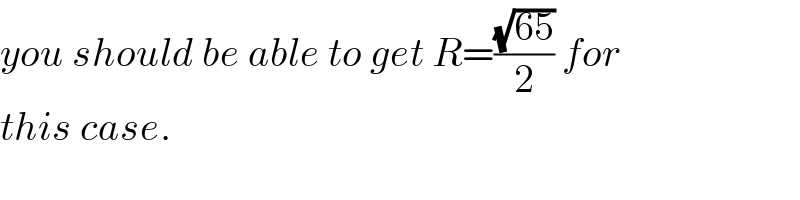
$${you}\:{should}\:{be}\:{able}\:{to}\:{get}\:{R}=\frac{\sqrt{\mathrm{65}}}{\mathrm{2}}\:{for} \\ $$$${this}\:{case}. \\ $$
Commented by I want to learn more last updated on 10/Apr/21

$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
