Question Number 95378 by Fikret last updated on 24/May/20
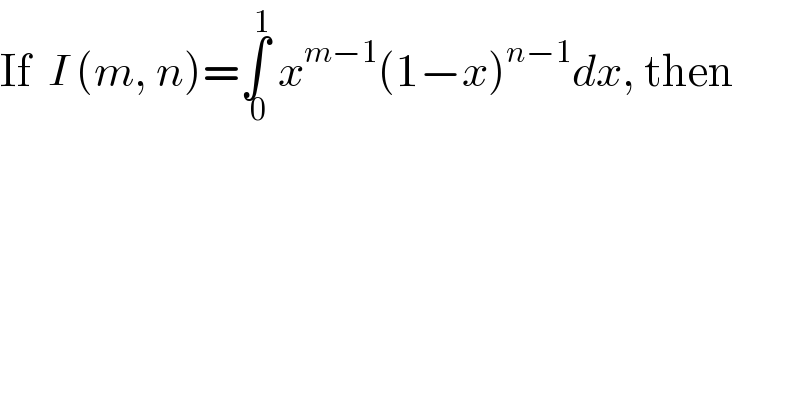
$$\mathrm{If}\:\:{I}\:\left({m},\:{n}\right)=\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}^{{m}−\mathrm{1}} \left(\mathrm{1}−{x}\right)^{{n}−\mathrm{1}} {dx},\:\mathrm{then} \\ $$
Commented by Tony Lin last updated on 24/May/20

$${then}\:{I}\left({m},{n}\right)\:{is}\:{a}\:{Beta}\:{function} \\ $$
Answered by mathmax by abdo last updated on 25/May/20
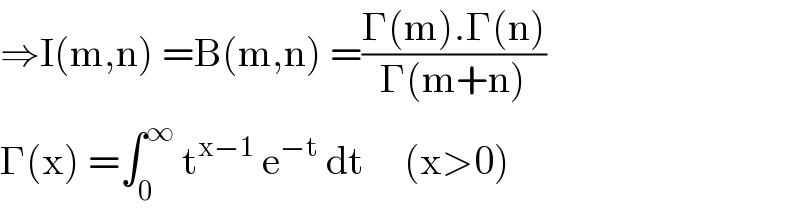
$$\Rightarrow\mathrm{I}\left(\mathrm{m},\mathrm{n}\right)\:=\mathrm{B}\left(\mathrm{m},\mathrm{n}\right)\:=\frac{\Gamma\left(\mathrm{m}\right).\Gamma\left(\mathrm{n}\right)}{\Gamma\left(\mathrm{m}+\mathrm{n}\right)} \\ $$$$\Gamma\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\:\:\:\:\left(\mathrm{x}>\mathrm{0}\right) \\ $$
