Question Number 106666 by deep last updated on 06/Aug/20

$$\mathrm{In}\:\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{8}\:\mathrm{and}\:\:\mathrm{5}{x}+{Ky}=\mathrm{3},\:\mathrm{find}\:\mathrm{the} \\ $$$$\mathrm{value}\:\mathrm{of}\:{K}\:\mathrm{so}\:\mathrm{that}\:\mathrm{the}\:\mathrm{given}\:\mathrm{system} \\ $$$$\mathrm{of}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{infinte}\:\mathrm{solution}. \\ $$
Commented by bemath last updated on 06/Aug/20

$$\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\:\mathrm{3}}\\{\mathrm{5}\:\:\:\:\:\:\mathrm{k}}\end{pmatrix}\:\begin{pmatrix}{\mathrm{x}}\\{\mathrm{y}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{8}}\\{\mathrm{3}}\end{pmatrix} \\ $$$$\mathrm{has}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{if}\:\Delta\:=\:\mathrm{0}\: \\ $$$$\Rightarrow\mathrm{2k}−\mathrm{15}\:=\:\mathrm{0}\:,\:\mathrm{k}\:=\:\frac{\mathrm{15}}{\mathrm{2}} \\ $$
Commented by Her_Majesty last updated on 06/Aug/20
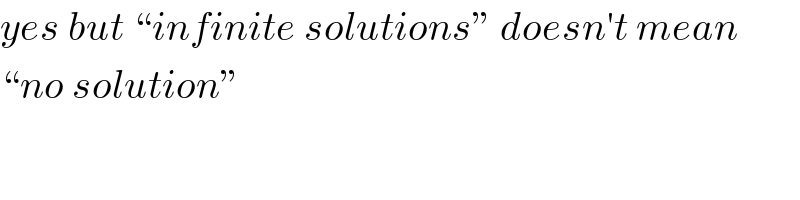
$${yes}\:{but}\:“{infinite}\:{solutions}''\:{doesn}'{t}\:{mean} \\ $$$$“{no}\:{solution}'' \\ $$
Answered by nimnim last updated on 06/Aug/20

$${The}\:{equations}\:{will}\:{have}\:{infinite}\:{solution}\:{if} \\ $$$$\frac{{a}_{\mathrm{1}} }{{a}_{\mathrm{2}} }=\frac{{b}_{\mathrm{1}} }{{b}_{\mathrm{2}} }=\frac{{c}_{\mathrm{1}} }{{c}_{\mathrm{2}} }\:\:\:{i}.{e}\:\frac{\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{3}}{{k}}=\frac{\mathrm{8}}{\mathrm{3}}\Rightarrow\mathrm{1}=\frac{\mathrm{5}}{\mathrm{3}}×\frac{\mathrm{3}}{{k}}×\frac{\mathrm{3}}{\mathrm{8}}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}=\frac{\mathrm{15}}{\mathrm{8}{k}}=\mathrm{1}\Rightarrow{k}=\frac{\mathrm{15}}{\mathrm{8}} \\ $$
Commented by Her_Majesty last updated on 06/Aug/20

$${wrong}.\:{with}\:{k}=\frac{\mathrm{15}}{\mathrm{8}}\:{we}\:{get}\:{x}=−\frac{\mathrm{8}}{\mathrm{15}}\wedge{y}=\frac{\mathrm{136}}{\mathrm{45}} \\ $$$${which}\:{is}\:{a}\:{unique}\:{solution} \\ $$
Answered by Her_Majesty last updated on 06/Aug/20

$$\begin{cases}{\mathrm{2}{x}+\mathrm{3}{y}=\mathrm{8}}\\{\mathrm{5}{x}+{Ky}=\mathrm{3}}\end{cases}\:\Leftrightarrow\:\begin{cases}{{y}=−\frac{\mathrm{2}}{\mathrm{3}}{x}+\frac{\mathrm{8}}{\mathrm{3}}}\\{{y}=−\frac{\mathrm{5}}{{k}}{x}+\frac{\mathrm{3}}{{k}}}\end{cases} \\ $$$${both}\:{are}\:{linear}\:\Rightarrow\:{infinite}\:{solutions}\:{if} \\ $$$$\left({I}\right)\:=\:\left({II}\right)\:{which}\:{is}\:{impossible}\:{if}\:{K}\in\mathbb{C}: \\ $$$$> \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}}=−\frac{\mathrm{5}}{{K}}\wedge\frac{\mathrm{8}}{\mathrm{3}}=\frac{\mathrm{3}}{{K}} \\ $$$${K}=\frac{\mathrm{15}}{\mathrm{2}}\wedge{K}=\frac{\mathrm{9}}{\mathrm{8}}\:{which}\:{is}\:{impossible} \\ $$$${if}\:{K}\:{is}\:{not}\:{a}\:{number} \\ $$$$−\frac{\mathrm{2}}{\mathrm{3}}{x}+\frac{\mathrm{8}}{\mathrm{3}}=−\frac{\mathrm{5}}{{K}}{x}+\frac{\mathrm{3}}{{K}} \\ $$$$\Rightarrow \\ $$$${K}=\frac{\mathrm{3}\left(\mathrm{5}{x}−\mathrm{3}\right)}{\mathrm{2}\left({x}−\mathrm{4}\right)} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{y}=−\frac{\mathrm{2}}{\mathrm{3}}{x}+\frac{\mathrm{8}}{\mathrm{3}}}\\{{y}=−\frac{\mathrm{2}}{\mathrm{3}}{x}+\frac{\mathrm{8}}{\mathrm{3}}}\end{cases} \\ $$
