Question Number 43624 by peter frank last updated on 12/Sep/18
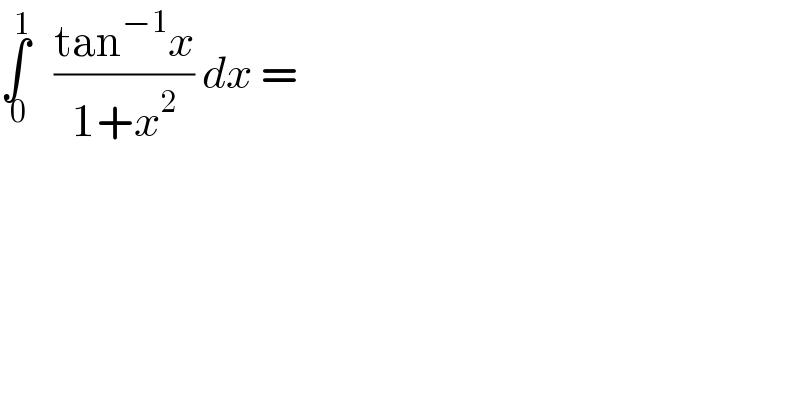
$$\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\:\frac{\mathrm{tan}^{−\mathrm{1}} {x}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:= \\ $$
Commented by math khazana by abdo last updated on 13/Sep/18
![let I = ∫_0 ^1 ((arctanx)/(1+x^2 ))dx let integrate by parts u^′ =(1/(1+x^2 )) and v^ =arctanx ⇒ I =[arctan^2 x]_0 ^1 −∫_0 ^1 ((arctanx)/(1+x^2 ))dx =(π^2 /(16)) −I ⇒ 2I=(π^2 /(16)) ⇒I =(π^2 /(32)) .](https://www.tinkutara.com/question/Q43631.png)
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{let}\:{integrate}\:{by}\:{parts} \\ $$$${u}^{'} =\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:{and}\:{v}^{} ={arctanx}\:\Rightarrow \\ $$$${I}\:=\left[{arctan}^{\mathrm{2}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctanx}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:−{I}\:\Rightarrow \\ $$$$\mathrm{2}{I}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}\:\Rightarrow{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}\:. \\ $$
Answered by username last updated on 13/Sep/18

$$ \\ $$
