Question Number 66055 by ajfour last updated on 08/Aug/19

Commented by ajfour last updated on 08/Aug/19
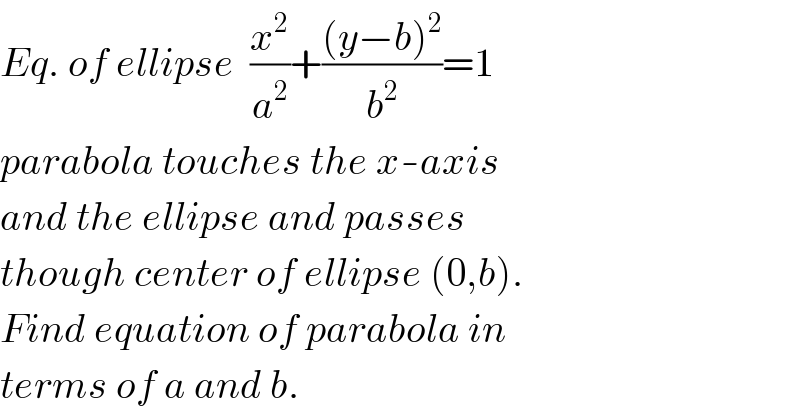
$${Eq}.\:{of}\:{ellipse}\:\:\frac{{x}^{\mathrm{2}} }{{a}^{\mathrm{2}} }+\frac{\left({y}−{b}\right)^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{1} \\ $$$${parabola}\:{touches}\:{the}\:{x}-{axis} \\ $$$${and}\:{the}\:{ellipse}\:{and}\:{passes} \\ $$$${though}\:{center}\:{of}\:{ellipse}\:\left(\mathrm{0},{b}\right). \\ $$$${Find}\:{equation}\:{of}\:{parabola}\:{in} \\ $$$${terms}\:{of}\:{a}\:{and}\:{b}. \\ $$
Answered by mr W last updated on 09/Aug/19
![eqn. of parabola: y=b(1−(x/p))^2 eqn. of ellipse: ((x/a))^2 +((y/b)−1)^2 =1 touch point P(h,k) let m=tan θ for tangent at touch point y′=−((2b)/p)(1−(h/p))=m ⇒h=p(1+((pm)/(2b))) (x/a^2 )+(1/b)((y/b)−1)y′=0 (h/a^2 )+(1/b)((k/b)−1)m=0 ⇒k=b[1−((pb)/(ma^2 ))(1+((pm)/(2b)))] ((h/a))^2 +((k/b)−1)^2 =1 ⇒(p^2 /a^2 )(1+(b^2 /(m^2 a^2 )))(1+((pm)/(2b)))^2 =1 ...(i) (k/b)=(1−(h/p))^2 ⇒1−((pb)/(ma^2 ))(1+((pm)/(2b)))=(((pm)/(2b)))^2 ...(ii) let λ=(p/a), μ=(b/a) from (i): ⇒λ^2 (1+(μ^2 /m^2 ))(1+((mλ)/(2μ)))^2 =1 ...(I) from (ii): ⇒1−((μλ)/m)(1+((mλ)/(2μ)))=(((mλ)/(2μ)))^2 ⇒(2+(m^2 /μ^2 ))λ^2 +((4μ)/m)λ−4 =0 ...(II) ⇒λ=(((2m)/μ)/(2+(m^2 /μ^2 )))=((2μm)/(2μ^2 +m^2 )) or m^2 −((2μ)/λ)m+2μ^2 =0 ⇒(m/μ)=(1/λ)(1+(√(1−2λ^2 ))) put this into (I): ⇒((λ^2 (3+(√(1−2λ^2 )))^2 )/8)(2+(λ^2 /(1−λ^2 +(√(1−2λ^2 )))))=1 ⇒λ=0.5194 (constant, independent from μ!) ⇒p=λa=0.5194a eqn. of parabola: ⇒y=b(1−(x/(0.5194a)))^2](https://www.tinkutara.com/question/Q66076.png)
$${eqn}.\:{of}\:{parabola}: \\ $$$${y}={b}\left(\mathrm{1}−\frac{{x}}{{p}}\right)^{\mathrm{2}} \\ $$$${eqn}.\:{of}\:{ellipse}: \\ $$$$\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{y}}{{b}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$${touch}\:{point}\:{P}\left({h},{k}\right) \\ $$$${let}\:{m}=\mathrm{tan}\:\theta\:{for}\:{tangent}\:{at}\:{touch}\:{point} \\ $$$${y}'=−\frac{\mathrm{2}{b}}{{p}}\left(\mathrm{1}−\frac{{h}}{{p}}\right)={m} \\ $$$$\Rightarrow{h}={p}\left(\mathrm{1}+\frac{{pm}}{\mathrm{2}{b}}\right) \\ $$$$\frac{{x}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}}\left(\frac{{y}}{{b}}−\mathrm{1}\right){y}'=\mathrm{0} \\ $$$$\frac{{h}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}}\left(\frac{{k}}{{b}}−\mathrm{1}\right){m}=\mathrm{0} \\ $$$$\Rightarrow{k}={b}\left[\mathrm{1}−\frac{{pb}}{{ma}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{pm}}{\mathrm{2}{b}}\right)\right] \\ $$$$\left(\frac{{h}}{{a}}\right)^{\mathrm{2}} +\left(\frac{{k}}{{b}}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\frac{{p}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{b}^{\mathrm{2}} }{{m}^{\mathrm{2}} {a}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{{pm}}{\mathrm{2}{b}}\right)^{\mathrm{2}} =\mathrm{1}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\frac{{k}}{{b}}=\left(\mathrm{1}−\frac{{h}}{{p}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{1}−\frac{{pb}}{{ma}^{\mathrm{2}} }\left(\mathrm{1}+\frac{{pm}}{\mathrm{2}{b}}\right)=\left(\frac{{pm}}{\mathrm{2}{b}}\right)^{\mathrm{2}} \:\:\:…\left({ii}\right) \\ $$$${let}\:\lambda=\frac{{p}}{{a}},\:\mu=\frac{{b}}{{a}} \\ $$$${from}\:\left({i}\right): \\ $$$$\Rightarrow\lambda^{\mathrm{2}} \left(\mathrm{1}+\frac{\mu^{\mathrm{2}} }{{m}^{\mathrm{2}} }\right)\left(\mathrm{1}+\frac{{m}\lambda}{\mathrm{2}\mu}\right)^{\mathrm{2}} =\mathrm{1}\:\:\:\:…\left({I}\right) \\ $$$${from}\:\left({ii}\right): \\ $$$$\Rightarrow\mathrm{1}−\frac{\mu\lambda}{{m}}\left(\mathrm{1}+\frac{{m}\lambda}{\mathrm{2}\mu}\right)=\left(\frac{{m}\lambda}{\mathrm{2}\mu}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}+\frac{{m}^{\mathrm{2}} }{\mu^{\mathrm{2}} }\right)\lambda^{\mathrm{2}} +\frac{\mathrm{4}\mu}{{m}}\lambda−\mathrm{4}\:=\mathrm{0}\:\:\:…\left({II}\right) \\ $$$$\Rightarrow\lambda=\frac{\frac{\mathrm{2}{m}}{\mu}}{\mathrm{2}+\frac{{m}^{\mathrm{2}} }{\mu^{\mathrm{2}} }}=\frac{\mathrm{2}\mu{m}}{\mathrm{2}\mu^{\mathrm{2}} +{m}^{\mathrm{2}} } \\ $$$${or}\:{m}^{\mathrm{2}} −\frac{\mathrm{2}\mu}{\lambda}{m}+\mathrm{2}\mu^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{m}}{\mu}=\frac{\mathrm{1}}{\lambda}\left(\mathrm{1}+\sqrt{\mathrm{1}−\mathrm{2}\lambda^{\mathrm{2}} }\right) \\ $$$${put}\:{this}\:{into}\:\left({I}\right): \\ $$$$\Rightarrow\frac{\lambda^{\mathrm{2}} \left(\mathrm{3}+\sqrt{\mathrm{1}−\mathrm{2}\lambda^{\mathrm{2}} }\right)^{\mathrm{2}} }{\mathrm{8}}\left(\mathrm{2}+\frac{\lambda^{\mathrm{2}} }{\mathrm{1}−\lambda^{\mathrm{2}} +\sqrt{\mathrm{1}−\mathrm{2}\lambda^{\mathrm{2}} }}\right)=\mathrm{1} \\ $$$$\Rightarrow\lambda=\mathrm{0}.\mathrm{5194}\:\left({constant},\:{independent}\:{from}\:\mu!\right) \\ $$$$\Rightarrow{p}=\lambda{a}=\mathrm{0}.\mathrm{5194}{a} \\ $$$$ \\ $$$${eqn}.\:{of}\:{parabola}: \\ $$$$\Rightarrow{y}={b}\left(\mathrm{1}−\frac{{x}}{\mathrm{0}.\mathrm{5194}{a}}\right)^{\mathrm{2}} \\ $$
Commented by MJS last updated on 09/Aug/19
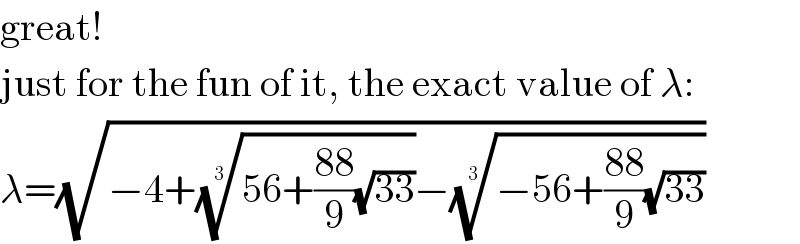
$$\mathrm{great}! \\ $$$$\mathrm{just}\:\mathrm{for}\:\mathrm{the}\:\mathrm{fun}\:\mathrm{of}\:\mathrm{it},\:\mathrm{the}\:\mathrm{exact}\:\mathrm{value}\:\mathrm{of}\:\lambda: \\ $$$$\lambda=\sqrt{−\mathrm{4}+\sqrt[{\mathrm{3}}]{\mathrm{56}+\frac{\mathrm{88}}{\mathrm{9}}\sqrt{\mathrm{33}}}−\sqrt[{\mathrm{3}}]{−\mathrm{56}+\frac{\mathrm{88}}{\mathrm{9}}\sqrt{\mathrm{33}}}} \\ $$
Commented by mr W last updated on 08/Aug/19

Commented by mr W last updated on 08/Aug/19

Commented by mr W last updated on 09/Aug/19
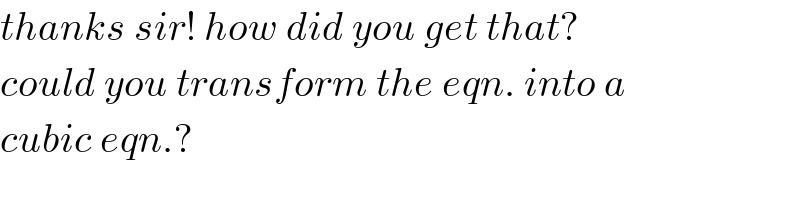
$${thanks}\:{sir}!\:{how}\:{did}\:{you}\:{get}\:{that}? \\ $$$${could}\:{you}\:{transform}\:{the}\:{eqn}.\:{into}\:{a} \\ $$$${cubic}\:{eqn}.? \\ $$
Commented by MJS last updated on 12/Aug/19

$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{get}\:\mathrm{no}\:\mathrm{notifications}\:\mathrm{again}… \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{transform}\:\mathrm{to} \\ $$$$\lambda^{\mathrm{6}} +\mathcal{A}\lambda^{\mathrm{4}} +\mathcal{B}\lambda^{\mathrm{2}} +\mathcal{C}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{then}\:\mathrm{follow}\:\mathrm{the}\:\mathrm{usual}\:\mathrm{path} \\ $$
Commented by mr W last updated on 14/Aug/19
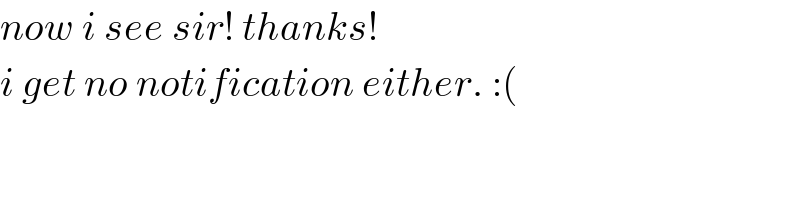
$${now}\:{i}\:{see}\:{sir}!\:{thanks}! \\ $$$${i}\:{get}\:{no}\:{notification}\:{either}.\::\left(\right. \\ $$
