Menu Close

If-tan-2-tan-2-tan-2-tan-2-tan-2-tan-2-2tan-2-tan-2-tan-2-1-then-the-value-of-sin-2-sin-2-sin-2-is-

Tinku Tara 0 Comments
Pin




Question Number 46483 by peter frank last updated on 27/Oct/18
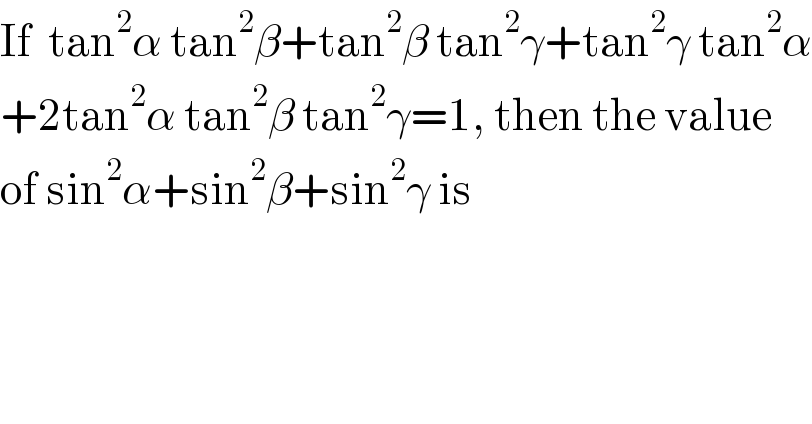
If tan^2 α tan^2 β+tan^2 β tan^2 γ+tan^2 γ tan^2 α +2tan^2 α tan^2 β tan^2 γ=1, then the value of sin^2 α+sin^2 β+sin^2 γ is
$$\mathrm{If}\:\:\mathrm{tan}^{\mathrm{2}} \alpha\:\mathrm{tan}^{\mathrm{2}} \beta+\mathrm{tan}^{\mathrm{2}} \beta\:\mathrm{tan}^{\mathrm{2}} \gamma+\mathrm{tan}^{\mathrm{2}} \gamma\:\mathrm{tan}^{\mathrm{2}} \alpha \\ $$$$+\mathrm{2tan}^{\mathrm{2}} \alpha\:\mathrm{tan}^{\mathrm{2}} \beta\:\mathrm{tan}^{\mathrm{2}} \gamma=\mathrm{1},\:\mathrm{then}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \beta+\mathrm{sin}^{\mathrm{2}} \gamma\:\mathrm{is} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Oct/18
tanα=a tanβ=b tanγ=c a^2 b^2 +b^2 c^2 +a^2 c^2 +2a^2 b^2 c^2 =1←(1) to find (a^2 /(a^2 +1))+(b^2 /(b^2 +1))+(c^2 /(c^2 +1))=? now from (1) we get (1/a^2 )+(1/b^2 )+(1/c^2 )+2=(1/(a^2 b^2 c^2 )) now say k=(a^2 /(a^2 +1))+(b^2 /(b^2 +1))+(c^2 /(c^2 +1)) k=((a^2 (b^2 +1)(c^2 +1)+b^2 (a^2 +1)(c^2 +1)+c^2 (a^2 +1)(b^2 +1))/((a^2 +1)(b^2 +1)(c^2 +1))) ((a^2 (b^2 c^2 +b^2 +c^2 +1)+b^2 (a^2 c^2 +a^2 +c^2 +1)+c^2 (a^2 b^2 +a^2 +b^2 +1))/(a^2 (b^2 c^2 +b^2 +c^2 +1)+b^2 c^2 +b^2 +c^2 +1)) =((3a^2 b^2 c^2 +2(a^2 b^2 +b^2 c^2 +a^2 c^2 )+a^2 +b^2 +c^2 )/(a^2 b^2 c^2 +a^2 b^2 +a^2 c^2 +b^2 c^2 +a^2 +b^2 +c^2 +1)) =((3a^2 b^2 c^2 +2(a^2 b^2 +b^2 c^2 +a^2 c^2 )+a^2 +b^2 +c^2 )/(3a^2 b^2 c^2 +2(a^2 b^2 +b^2 c^2 +a^2 c^2 )+a^2 +b^2 +c^2 )) (putting the value of 1 in denominator a^2 b^2 +b^2 c^2 +a^2 c^2 +2a^2 b^2 c^2 =1) =1
$${tan}\alpha={a}\:\:\:{tan}\beta={b}\:\:\:{tan}\gamma={c} \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{1}\leftarrow\left(\mathrm{1}\right) \\ $$$${to}\:{find} \\ $$$$\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{1}}+\frac{{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{1}}+\frac{{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} +\mathrm{1}}=? \\ $$$${now}\:{from}\:\left(\mathrm{1}\right)\:{we}\:{get} \\ $$$$\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\mathrm{2}=\frac{\mathrm{1}}{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} } \\ $$$${now}\:{say} \\ $$$${k}=\frac{{a}^{\mathrm{2}} }{{a}^{\mathrm{2}} +\mathrm{1}}+\frac{{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} +\mathrm{1}}+\frac{{c}^{\mathrm{2}} }{{c}^{\mathrm{2}} +\mathrm{1}} \\ $$$${k}=\frac{{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} +\mathrm{1}\right)\left({c}^{\mathrm{2}} +\mathrm{1}\right)+{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({c}^{\mathrm{2}} +\mathrm{1}\right)+{c}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right)}{\left({a}^{\mathrm{2}} +\mathrm{1}\right)\left({b}^{\mathrm{2}} +\mathrm{1}\right)\left({c}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$\frac{{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{1}\right)+{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{1}\right)+{c}^{\mathrm{2}} \left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{1}\right)}{{a}^{\mathrm{2}} \left({b}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{1}\right)+{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{3}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} } \\ $$$$\left({putting}\:{the}\:{value}\:{of}\:\mathrm{1}\:{in}\:{denominator}\right. \\ $$$$\left.{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {c}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} =\mathrm{1}\right) \\ $$$$=\mathrm{1} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *