Question Number 50132 by CIRCLE001 last updated on 14/Dec/18
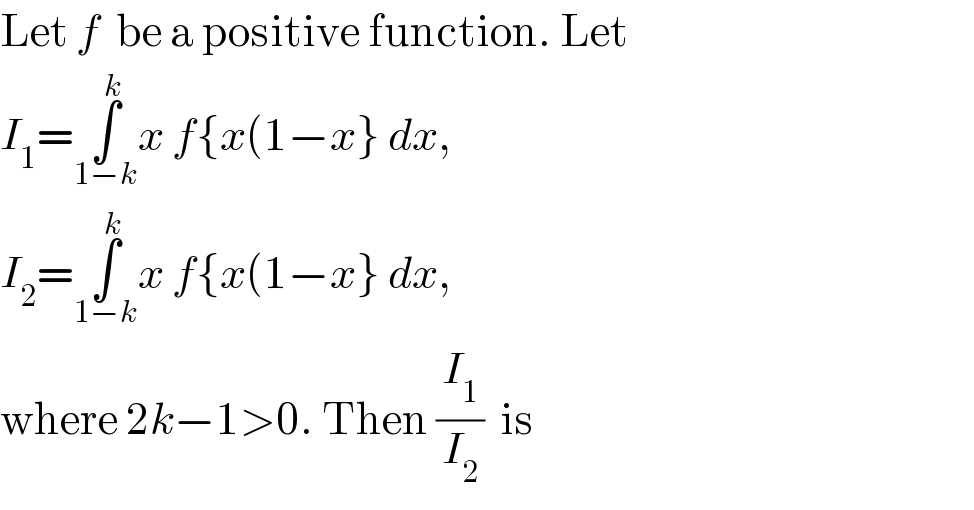
$$\mathrm{Let}\:{f}\:\:\mathrm{be}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{function}.\:\mathrm{Let} \\ $$$${I}_{\mathrm{1}} =\underset{\mathrm{1}−{k}} {\overset{{k}} {\int}}{x}\:{f}\left\{{x}\left(\mathrm{1}−{x}\right\}\:{dx},\:\right. \\ $$$${I}_{\mathrm{2}} =\underset{\mathrm{1}−{k}} {\overset{{k}} {\int}}{x}\:{f}\left\{{x}\left(\mathrm{1}−{x}\right\}\:{dx},\:\right. \\ $$$$\mathrm{where}\:\mathrm{2}{k}−\mathrm{1}>\mathrm{0}.\:\mathrm{Then}\:\frac{{I}_{\mathrm{1}} }{{I}_{\mathrm{2}} }\:\:\mathrm{is} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 14/Dec/18
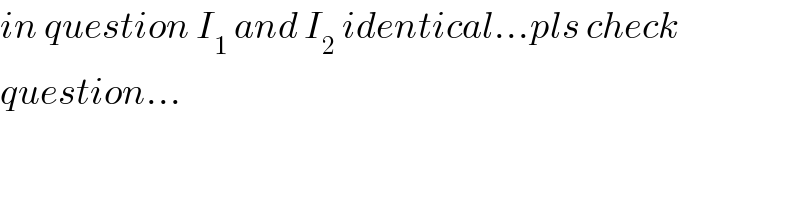
$${in}\:{question}\:{I}_{\mathrm{1}} \:{and}\:{I}_{\mathrm{2}} \:{identical}…{pls}\:{check}\: \\ $$$${question}… \\ $$
